cs336 assignment2

End to End benchmarking

Measuring performance is subtle — some common traps can cause us to not measure what we want. For benchmarking GPU code, one caveat is that CUDA calls are asynchronous. When you call a CUDA kernel,such as when you invoke torch.matmul, the function call returns control to your code without waiting for the matrix multiplication to finish. In this way, the CPU can continue running while the GPU computes the matrix multiplication. On the other hand, this means that naïvely measuring how long the torch.matmul call takes to return does not tell us how long the GPU takes to actually run the matrix multiplication In PyTorch, we can call torch.cuda.synchronize() to wait for all GPU kernels to complete, allowing us to get more accurate measurements of CUDA kernel runtime. With this in mind, let’s write our basic profiling infrastructure

测量性能是非常微妙的，一些常见的陷阱会导致我们没能测出我们想要的。例如测试 GPU 代码，一个忠告是 CUDA 调用是异步的。当你调用一个 CUDA kernel，例如当你调用矩阵乘法，函数会将控制权返回给你接下来的代码不等矩阵乘法结束。在这种方式下，CPU 能够继续运行与此同时 GPU 在计算矩阵乘法。另一方面这意味着普通的测试 torch.matmul 花费不能告诉我们 GPU 花费的实际时间。不过，我们就可以调用 torch.cuda.synchronize() 来等待所有的 GPU 核心来计算完成，这允许我们来获得更准确的 CUDA 核心运行时间测量。在了解这些后，让我们来写一些基础的性能分析框架吧。

Nsignt Systems Profiler

端到端基准测试无法显示模型在前向和反向传播过程中具体在哪些部分消耗时间和内存，因此无法揭示具体的优化机会。为了了解程序在每个组件（如函数）中花费的时间，我们可以使用性能分析器（profiler）。执行分析器通过在函数开始和结束时插入监控点来检测代码，从而提供函数级别的详细执行统计数据（如调用次数、平均耗时、累计耗时等）。

标准的 Python 分析器（如 CProfile）无法分析 CUDA 内核，因为这些内核是在 GPU 上异步执行的。幸运的是，NVIDIA 提供了一个可以通过命令行工具 nsys 使用的分析器，我们已经为您安装好了。在作业的这一部分，您将使用 nsys 来分析 Transformer 模型的运行时性能。使用 nsys 非常简单：只需在运行 Python 脚本时在前面加上 nsys profile 命令。例如，您可以通过以下命令分析 benchmark.py 脚本，并将输出写入 result.nsys.rep 文件：

Lec 2

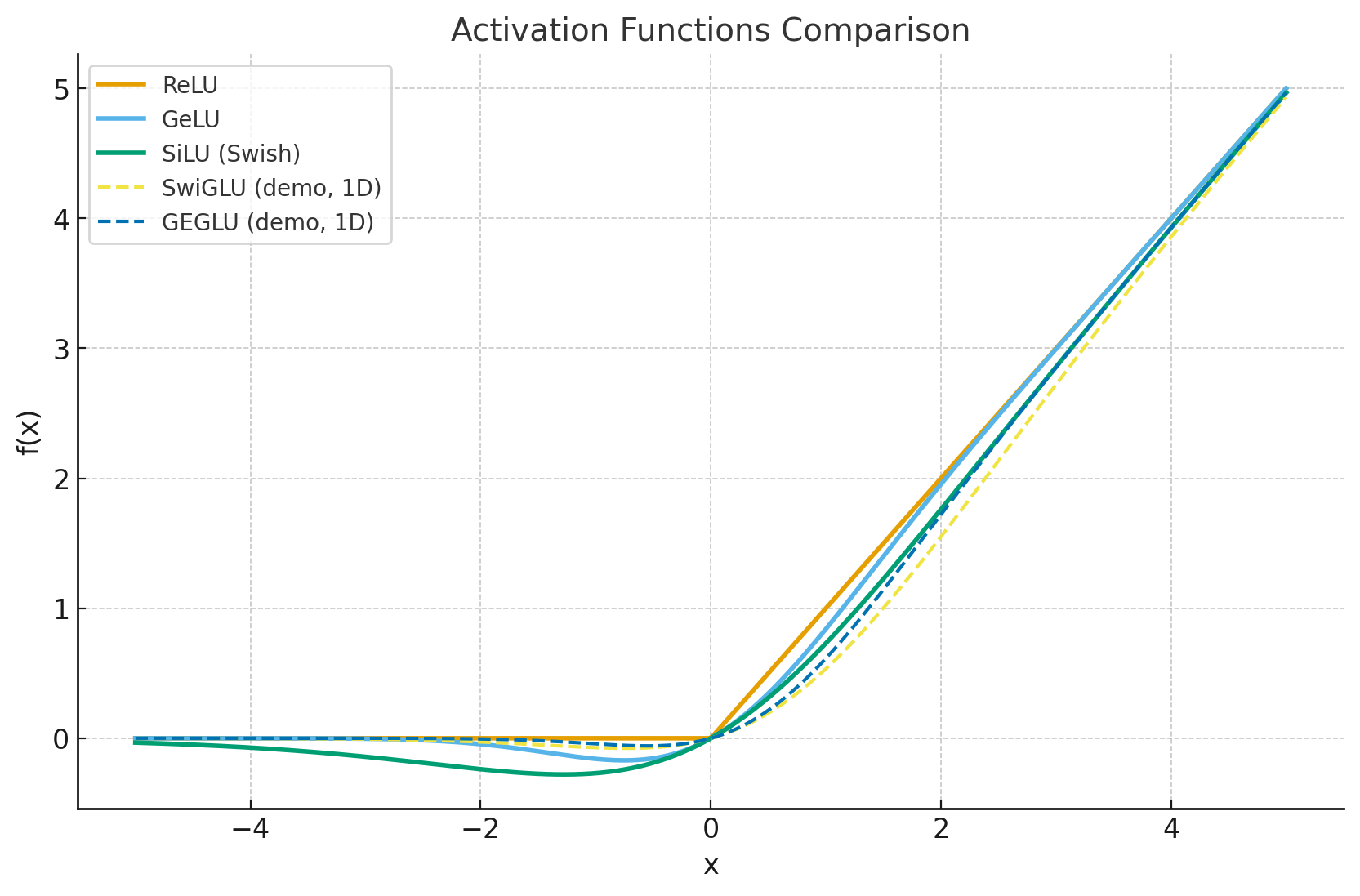
一些激活函数

我在你的作业讲义里找到了关于 ReLU、SiLU (Swish)、GLU、SwiGLU 的详细介绍，但 GeLU 和 GEGLU 没有直接提到，所以我会结合外部的知识来补充说明。下面总结一下四个激活函数/变体的要点：

---

1. ReLU (Rectified Linear Unit)

• 定义:

  $$\text{ReLU}(x)=\max (0,x)$$

• 特点: 简单高效，梯度传播清晰，但在负区间会出现“神经元死亡”问题。

• Transformer 使用: 原始 Transformer 的前馈层 (FFN) 就是使用 ReLU。

---

2. GeLU (Gaussian Error Linear Unit)

• 定义:

  $$\text{GeLU}(x)=x\cdot \Phi (x)$$

  其中 $\Phi (x)$ 是标准高斯分布的累积分布函数 (CDF)。 一个常见近似式：

  $$\text{GeLU}(x)\approx 0.5x\left(1+\tanh (\sqrt{2/\pi }(x+0.044715x^3))\right)$$

• 特点: 平滑地在负数区间削弱输入（而不是像 ReLU 那样直接截断）。在 BERT 等模型中表现优于 ReLU。

---

3. SwiGLU (Swish + GLU)

• 背景: 现代大模型常用 激活函数替代 + 门控机制。

• 组成部分:

  • SiLU/Swish:

    $$\text{SiLU}(x)=x\cdot \sigma (x)=\frac{x}{1+e^{-x}}$$

    它类似 ReLU，但在 0 附近平滑。

  • GLU (Gated Linear Unit):

    $$\text{GLU}(x;W_1,W_2)=\sigma (W_{1}x)\odot W_{2}x$$

    其中 $\odot$ 是逐元素乘法。

• SwiGLU 定义:

  \text{SwiGLU}(x; W_1,W_2,W_3) = W_2 \big( \text{SiLU}(W_1x) \odot W_3x \big) \

• 特点: 在 PaLM、LLaMA、Qwen 等 LLM 中广泛应用，实验表明比 ReLU/SiLU 更优。

---

4. GEGLU (GeLU + GLU)

• 定义: 把 SwiGLU 里的 SiLU 换成 GeLU：

  $$\text{GEGLU}(x;W_1,W_2,W_3)=W_2(\text{GeLU}(W_{1}x)\odot W_{3}x)$$

• 特点: 由 Shazeer (2020) 提出，同样利用门控机制，只是用 GeLU 替代了 SiLU。

• 使用场景: 在一些大型预训练模型中测试过，通常比单独的 GeLU 更好。

---

✅ 总结：

• ReLU → 简单快速，原始 Transformer 默认。
• GeLU → 平滑概率化 ReLU，BERT 等常用。
• SwiGLU → SiLU + 门控 (现代 LLM 默认)。
• GEGLU → GeLU + 门控 (SwiGLU 的近亲)。

要点在于：现代 LLM 更倾向于带门控的 SwiGLU/GEGLU，而不是单纯 ReLU/GeLU，因为门控增强了梯度流和表达能力。

---

好问题 👍。在训练 Transformer 或其他神经网络时，反向传播需要计算各激活函数的导数。下面我逐个介绍 ReLU、GeLU、SwiGLU、GEGLU 的反向传播实现。

---

1. ReLU

• 前向：

$$f(x)=\max (0,x)$$

• 导数：

$$f^{\prime }(x)=\{\begin{array}{ll}1& x>0\\ 0& x\le 0\end{array}$$

• 反向传播实现：只需保存前向时 $x>0$ 的 mask。

def relu_backward(grad_out, x):
    grad_x = grad_out * (x > 0).astype(float)
    return grad_x

---

2. GeLU

• 前向 (近似公式)：

$$f(x)=0.5x(1+\tanh (\sqrt{\frac{2}{\pi }}(x+0.044715x^3)))$$

• 导数：稍复杂，可以分解为

$$f^{\prime }(x)=\Phi (x)+x\cdot \varphi (x)$$

其中 $\Phi (x)$ 是标准正态 CDF，$\varphi (x)$ 是标准正态 PDF。 在实际实现时用近似公式的导数：

def gelu_backward(grad_out, x):
    # 常数
    k = np.sqrt(2/np.pi)
    inner = k * (x + 0.044715 * x**3)
    tanh_inner = np.tanh(inner)
    sech2_inner = 1 - tanh_inner**2
    
    grad = 0.5 * (1 + tanh_inner + x * sech2_inner * k * (1 + 3*0.044715*x**2))
    return grad_out * grad

---

3. SwiGLU

• 前向：

$$\text{SwiGLU}(x;W_1,W_2,W_3)=W_2(\text{SiLU}(W_{1}x)\odot W_{3}x)$$

其中

$$\text{SiLU}(u)=u\cdot \sigma (u),\sigma (u)=\frac{1}{1+e^{-u}}$$

• 导数（关键部分）：

  • 对 $u=W_{1}x$：

    $$\frac{\partial \text{SiLU}(u)}{\partial u}=\sigma (u)+u\cdot \sigma (u)(1-\sigma (u))$$

  • 然后应用链式法则，把梯度传播到 $W_1,W_2,W_3,x$。

• 反向传播实现（简化 1 D demo）：

def silu_backward(grad_out, u):
    sig = 1 / (1 + np.exp(-u))
    grad = sig + u * sig * (1 - sig)
    return grad_out * grad

在 SwiGLU 中，还要额外乘上另一分支 $W_{3}x$，再传播到 $W_1,W_2,W_3$。

---

4. GEGLU

• 前向：

$$\text{GEGLU}(x;W_1,W_2,W_3)=W_2(\text{GeLU}(W_{1}x)\odot W_{3}x)$$

• 导数：

  • 对 $u=W_{1}x$：

    $$\frac{\partial \text{GeLU}(u)}{\partial u}=\Phi (u)+u\cdot \varphi (u)$$

  • 然后同样用链式法则传播。

• 反向传播实现（简化 1 D demo）：

def gelu_derivative(x):
    # phi(x): PDF, Phi(x): CDF
    phi = np.exp(-0.5*x**2) / np.sqrt(2*np.pi)
    Phi = 0.5 * (1 + torch.erf(x / np.sqrt(2)))
    return Phi + x * phi

在 GEGLU 中，梯度需要和另一分支 $W_{3}x$ 相乘再反传。

---

✅ 总结：

• ReLU: 梯度是 {0,1} 的二值 mask。
• GeLU: 梯度涉及高斯 CDF/PDF，平滑但计算比 ReLU 复杂。
• SwiGLU / GEGLU: 梯度需要对 门控分支和主分支分别反传，用链式法则组合，计算成本比单一激活高。

---

非常好的问题！我们来仔细讲一下 GeLU 近似实现公式 是怎么被“想出来的”。

---

1. 精确形式太复杂

我们知道 GeLU 的精确形式是：

$$\text{GeLU}(x)=x\cdot \Phi (x),f^{\prime }(x)=\Phi (x)+x\varphi (x)$$

其中：

• $\Phi (x)=\frac{1}{2}(1+\mathrm{erf}(x/\sqrt{2}))$
• $\varphi (x)=\frac{1}{\sqrt{2\pi }}{e}^{-x^2/2}$

问题在于：

• 误差函数 erf 和 高斯密度函数 φ 在硬件上代价较高，不像 $\tanh$ 和 $\sigma$ 那样有高效近似实现。
• 在 GPU 上要做大规模训练，需要一个更快的近似公式。

---

2. 思路：用更快的函数近似 CDF

因为 $\Phi (x)$ 是 S 型曲线 (sigmoid-like)，可以尝试用 $\tanh$ 或 sigmoid 来逼近。

• $\tanh$ 的形状和高斯 CDF 很接近（都是平滑 S 曲线）。
• 所以 Hendrycks & Gimpel (2016) 提出：

$$\Phi (x)\approx 0.5(1+\tanh (a(x+b{x}^3)))$$

这里 $a$ 和 $b$ 是待拟合的参数。

---

3. 参数选择

通过拟合实验，发现：

• $a=\sqrt{2/\pi }\approx 0.79788456$
• $b=0.044715$

这个三次项 $0.044715x^3$ 用来改善在尾部区域的拟合效果（因为正态 CDF 在大数值时下降得比 $\tanh$ 更快）。

于是得到最终近似：

$$\Phi (x)\approx 0.5(1+\tanh (\sqrt{\frac{2}{\pi }}(x+0.044715x^3)\left)\right)$$

代入 GeLU：

$$\text{GeLU}(x)\approx 0.5x(1+\tanh (\sqrt{\frac{2}{\pi }}(x+0.044715x^3)\left)\right)$$

---

4. 为什么有效

• 这个公式在数值上非常接近真实 GeLU，最大误差很小。
• $\tanh$ 的梯度容易计算，GPU 上实现效率高。
• 保持了 GeLU 的“平滑过渡”特性，又避免了复杂的高斯函数运算。

---

✅ 总结： GeLU 的近似公式是通过 用 $\tanh$ 来逼近正态分布 CDF，再加上三次项微调尾部形状，从而得到既快又准的近似。

这个问题问得很关键 👍。为什么 GLU (Gated Linear Unit) 及其变体（SwiGLU, GEGLU 等）在 大模型 (LLM) 架构中成为主流选择？我总结几个核心原因：

---

1. 增强的表达能力 (Expressiveness)

• 普通激活函数 (ReLU/GeLU)：对每个神经元的输出做非线性变换，但不考虑输入的动态选择。

• GLU：在 FFN 中引入了 门控机制：

  $$\text{GLU}(x;W_1,W_2)=(W_{1}x)\odot \sigma (W_{2}x)$$
  • $W_{1}x$：主分支（主要特征流）。
  • $\sigma (W_{2}x)$：门控分支（决定保留/抑制多少信息）。

• 这使得 FFN 层能更灵活地“选择性通过信息”，增加了模型的非线性表达能力。

---

2. 改善梯度流动 (Gradient Flow)

• 在训练大模型时，梯度消失/爆炸是常见问题。
• 门控机制的 sigmoid/SiLU 保证梯度在负区间不会完全消失（不像 ReLU 那样硬截断）。
• 同时，主分支提供了“直通路径”，让梯度更稳定。

---

3. 参数利用效率更高

• GLU 结构相当于在 FFN 中引入 条件计算 (conditional computation)：不同输入会激活不同的“门”。

• 在相同的参数量下，模型的 容量 (capacity) 增强。

• 实验证明：SwiGLU/GEGLU 在相同 FLOPs 下，性能优于 ReLU/GeLU。

  • 例如：PaLM, LLaMA, Qwen 等模型报告，换成 SwiGLU 可以提升 perplexity/zero-shot 能力。

---

4. 更适合大规模训练的数值稳定性

• ReLU 在 0 以下完全“死亡”，GeLU 虽然平滑，但在极端值区间梯度也会很小。
• GLU 系列由于有门控和主分支相乘，能在训练时更平衡地传递信号，不容易“梯度稀疏”或“过大”。
• 在数百亿参数规模的模型中，这种稳定性至关重要。

---

5. 实践中的证据

• SwiGLU（用 SiLU 作为门控函数）：在 Google PaLM, Meta LLaMA, Qwen 等主流 LLM 中成为默认选择。
• GEGLU（用 GeLU 作为门控函数）：在一些模型中也有尝试，效果接近或略好于 GeLU。
• 报告结果：相比 ReLU/GeLU，GLU 变体几乎总是带来 更低的损失、更好的下游任务表现。

---

✅ 总结： GLU 之所以在大模型架构中成为主流，是因为它通过 门控机制 带来了：

1. 更强的表达能力（能动态选择信息）。
2. 更稳定的梯度传播。
3. 更高的参数利用效率。
4. 大规模训练下的数值稳定性。

因此，现代 LLM（PaLM、LLaMA、Qwen、Mistral 等）几乎都弃用了单一 ReLU/GeLU，转向 SwiGLU/GEGLU。

---

要不要我帮你整理一张 激活函数演进路线图（ReLU → GeLU → GLU → SwiGLU），直观展示它们是如何一步步成为 LLM 默认选择的？