LLM101

https://hanlab.mit.edu/courses/2024-fall-65940

TinyML and Efficient Deep Learning Computing

Transformer

Transformer是一种基于自注意力机制的神经网络架构，由Google在2017年提出。它最初用于自然语言处理任务，现在已经成为深度学习领域最重要的模型之一。

核心组件

1. 自注意力机制(Self-Attention)

   • 允许模型关注输入序列中的不同部分
   • 计算注意力权重来确定每个元素与其他元素的关联程度
   • 通过Query、Key、Value三个矩阵实现

2. 多头注意力(Multi-Head Attention)

   • 并行运行多个注意力机制
   • 允许模型同时关注不同的表示子空间
   • 增强模型的表达能力

3. 位置编码(Positional Encoding)

   • 为序列中的每个位置添加位置信息
   • 使模型能够理解元素的相对或绝对位置
   • 通常使用正弦和余弦函数实现

4. 前馈神经网络(Feed-Forward Network)

   • 对每个位置独立应用的全连接层
   • 增加模型的非线性变换能力

架构特点

• 编码器-解码器结构

  • 编码器处理输入序列
  • 解码器生成输出序列
  • 可以堆叠多层以增加模型深度

• 并行计算

  • 不同于RNN的顺序处理
  • 所有位置可以并行计算
  • 显著提高训练效率

• 长距离依赖

  • 直接建模序列中任意位置间的关系
  • 避免了RNN中的梯度消失问题
  • 更好地捕获长距离依赖关系

介绍注意力机制

注意力机制是Transformer的核心组件，它通过计算序列中不同位置之间的关联程度来加权信息。其基本形式可以表示为:

$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$

其中:

• Q (Query): 查询矩阵
• K (Key): 键矩阵
• V (Value): 值矩阵
• $d_k$: Key的维度
• $\sqrt{d_k}$: 缩放因子,用于梯度的稳定性

多头注意力机制则是将输入投影到多个子空间:

$MultiHead(Q,K,V)=Concat(hea{d}_1,...,hea{d}_h)W^O$

其中每个head计算如下:

$hea{d}_i=Attention(Q{W}_i^Q,K{W}_i^K,V{W}_i^V)$

这种机制允许模型:

• 在不同的表示子空间关注不同的模式
• 同时学习多种类型的依赖关系
• 增强特征提取的能力

位置编码

上面的很多内容来自于AI生成，下面开始介绍位置编码，首先说说我目前的理解，单纯的Attention模型面临一个问题就是具有全对称性，即无法区分输入中不同token的位置，所以需要为输入向量添加位置编码。 当然可以。我们来从头清晰、简洁地解释： 为什么如果没有位置编码，同一个词元在不同位置的输出是相同的。这其实是 Transformer 的一个核心性质。

---

🔍 1. 什么是“同一个词元在不同位置”？

假设句子是：

["dog", "chased", "dog"]

词“dog”出现在位置 0 和位置 2。我们使用词嵌入（embedding）将每个词转换为向量，比如：

x_0 = embedding("dog")
x_1 = embedding("chased")
x_2 = embedding("dog")

因为两个 “dog” 是同一个词，它们的向量是一样的：

x_0 == x_2

---

🔁 2. 自注意力是怎么计算的？

对于每个输入向量 $x_i$，我们要计算：

• Query: $q_i=x_i{W}_Q$
• Key: $k_i=x_i{W}_K$
• Value: $v_i=x_i{W}_V$

这些权重矩阵 $W_Q,W_K,W_V$ 是共享的，所以相同的输入 $x$ 计算出的 q/k/v 也一样。

因此：

x_0 == x_2 ⟹ q_0 == q_2, k_0 == k_2, v_0 == v_2

---

🎯 3. 看 Attention 是怎么作用的

自注意力计算方式：

$$\text{Attention}(Q,K,V)=\text{softmax}\left(\frac{Q{K}^{\top }}{\sqrt{d}}\right)V$$

假设你想计算第 $i$ 个位置的输出 $y_i$，它是：

$$y_i=\sum _j\text{softmax}\left(\frac{q_i\cdot k_j}{\sqrt{d}}\right)v_j$$

注意：这个输出仅依赖于 q_i、所有的 k_j 和所有的 v_j。

---

🧠 4. 关键点：对称性

我们现在考虑位置 0 和位置 2，它们都是 “dog”，也就是：

q_0 == q_2

而且 K 和 V 矩阵是整个序列里所有词元的 Key 和 Value 构成的，也一样：

整个序列没变，K 和 V 不变

所以：

softmax(q_0 ⋅ K^T) == softmax(q_2 ⋅ K^T)

最终加权求和也一样，所以：

y_0 == y_2

---

✅ 5. 结论

如果没有位置编码，那么同一个词元无论出现在第几个位置，计算出来的 Query、Key、Value 都是一样的，最终 Attention 输出也会一样。

换句话说：

Transformer 看不到词的位置，它只知道词的内容。 没有位置编码时，序列是“无序”的，对模型来说，“dog chased dog” 和 “dog dog chased” 是一样的。

---

💡 为何要加位置编码？

为了解决这个“词元不区分位置”的问题，Transformer 引入了位置编码（Positional Encoding），让：

• 不同位置的向量即使内容一样（比如两个“dog”），经过加上位置编码后变得不一样。
• 这样模型才知道哪个“dog”是句首的，哪个是句尾的。

---

Transformer学习笔记二：Self-Attention（自注意力机制）

目录

1. 一、笔记架构
2. 二、Attention构造
   1. 2.1 Attention的基本运作方式
   2. 2.2 Attention的计算过程图解
   3. 2.3 Masked Attention
   4. 2.4 Multihead Attention
3. 三、Attention代码实践
4. 四、参考

一、笔记架构

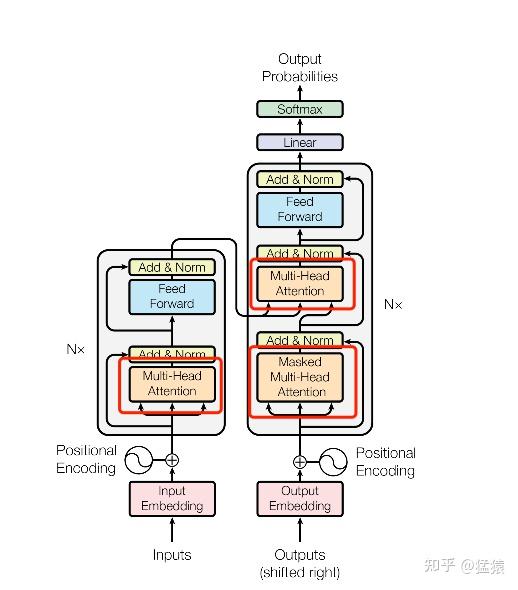
Transformer中的三处Attention

关于Transformer的系列笔记，预计出如下几篇：

1. Positional Encoding （位置编码），点击跳转
2. Self-attention（自注意力机制）
3. Batch Norm & Layer Norm（批量标准化/层标准化），点击跳转
4. ResNet（残差网络），点击跳转
5. Subword Tokenization（子词分词法），点击跳转
6. 组装：Transformer

在Transformer中，一共涉及到三个Attention零件。这篇笔记将基于这三个零件，对attention机制进行探讨，主要内容包括： （1）Attention机制的基本框架 （2）Attention Score的计算方法

• Dot product
• Additive product
• Scaled dot product (Transformer论文使用的方法，这里将探讨乘上因子 $1/{\sqrt{d}}_k$的意义） （3）Masked Attention （4）Multihead Attention实现方式及可视化（多头的意义） （5）Attention代码实践

二、Attention构造

2.1 Attention的基本运作方式

首先，来看RNN这样一个用于处理序列数据的经典模型。

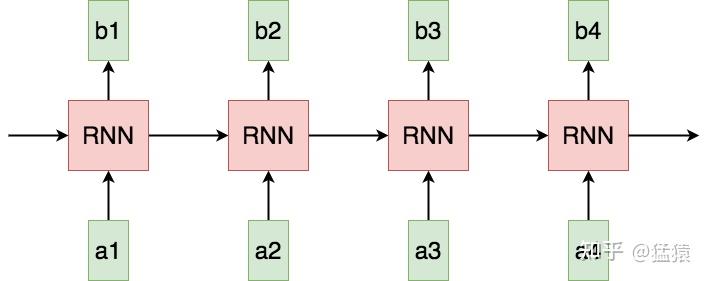
*图1: 传统RNN *

在RNN当中，tokens是一个一个被喂给模型的。比如在a3的位置，模型要等a1和a2的信息都处理完成后，才可以生成a3。这样的作用机制，使得RNN存在以下几个问题： (1) Sequential operations的复杂度随着序列长度的增加而增加。 这是指模型下一步计算的等待时间，在RNN中为O(N)。该复杂度越大，模型并行计算的能力越差，反之则反。 (2) Maximum Path length的复杂度随着序列长度的增加而增加。 这是指信息从一个数据点传送到另一个数据点所需要的距离，在RNN中同样为O(N)，距离越大，则在传送的过程中越容易出现信息缺失的情况，即数据点对于远距离处的信息，是很难“看见”的。

那么，在处理序列化数据的时候，是否有办法，在提升模型的并行运算能力的同时，对于序列中的每个token，也能让它不损失信息地看见序列里的其他tokens呢？

Attention就作为一种很好的改进办法出现了。

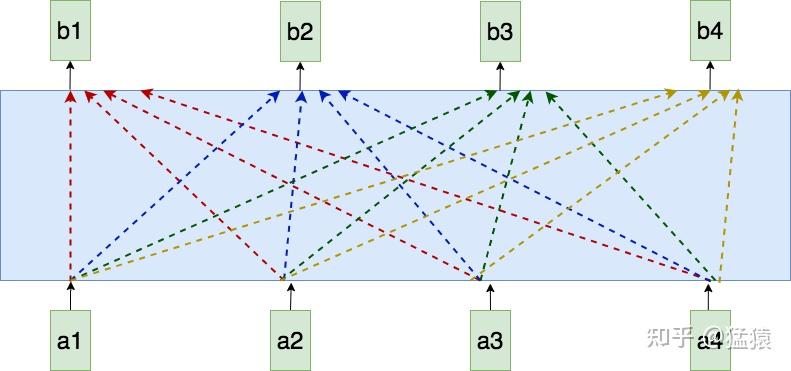
图2: Self-attention

如图，蓝色方框为一个attention模型。在每个位置，例如在a2处产生b2时，attention将会同时看过a1到a4的每个token。此外，每个token生成其对应的输出的过程是同时进行的，计算不需要等待。下面来看attention内部具体的运算过程。

2.2 Attention的计算过程图解

**2.2.1 Self-attention **

**（1）计算框架 **

Self-attention的意思是，我们给Attention的输入都来自同一个序列，其计算方式如下：

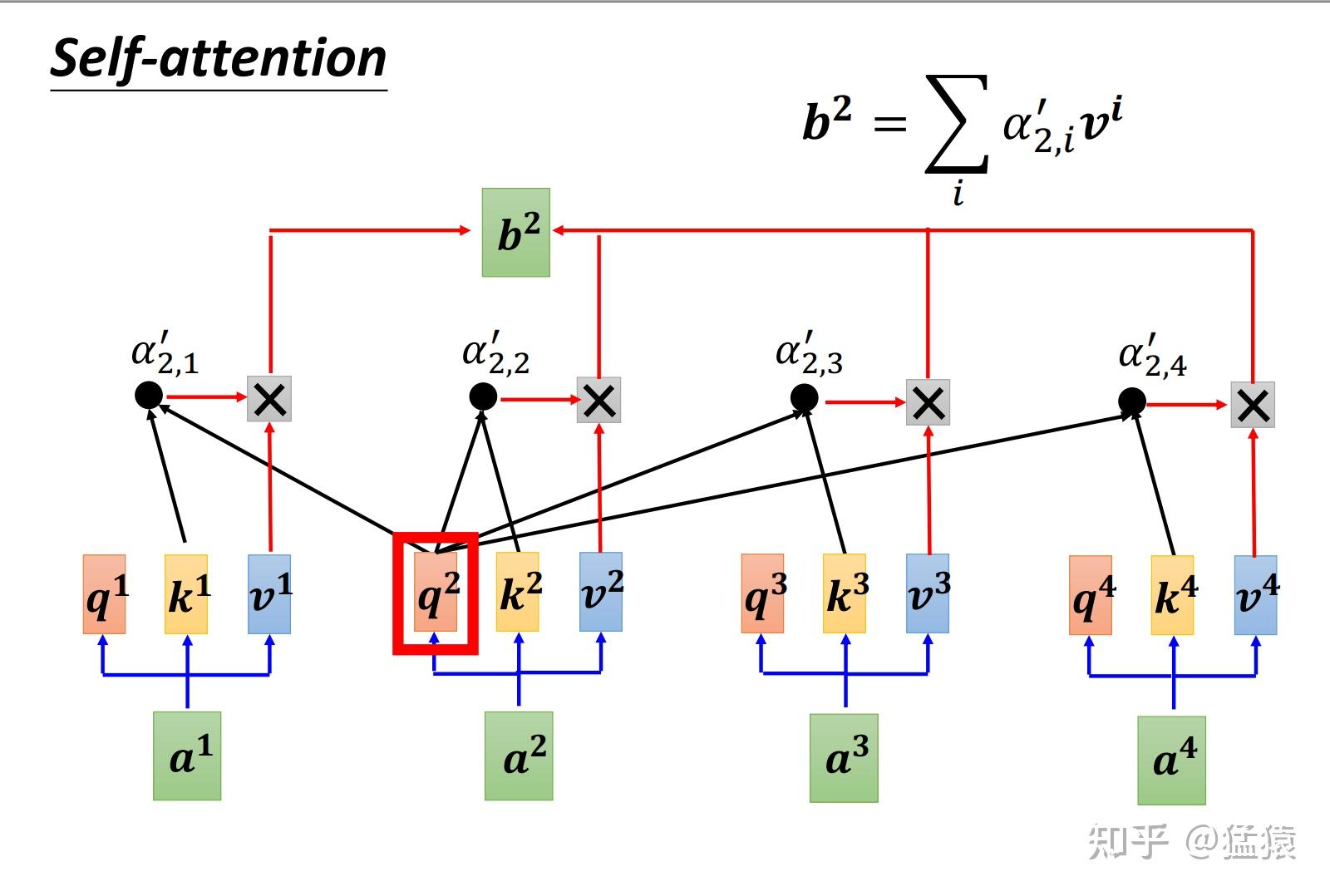
图3: self-attention计算框架 （图片来自李宏毅老师PPT）

这张图所表示的大致运算过程是： 对于每个token，先产生三个向量query，key，value：

• query向量类比于询问。某个token问：“其余的token都和我有多大程度的相关呀？”
• key向量类比于索引。某个token说：“我把每个询问内容的回答都压缩了下装在我的key里”
• value向量类比于回答。某个token说：“我把我自身涵盖的信息又抽取了一层装在我的value里”

以图中的token a2为例：

• 它产生一个query，每个query都去和别的token的key做“某种方式 ”的计算，得到的结果我们称为attention score（即为图中的$\alpha$）。则一共得到四个attention score。（attention score又可以被称为attention weight）。
• 将这四个score分别乘上每个token的value，我们会得到四个抽取信息完毕的向量。
• 将这四个向量相加，就是最终a2过attention模型后所产生的结果b2。

**（2）产生query，key和value **

下图描述了产生query(q)，key(k)和value(v)的过程：

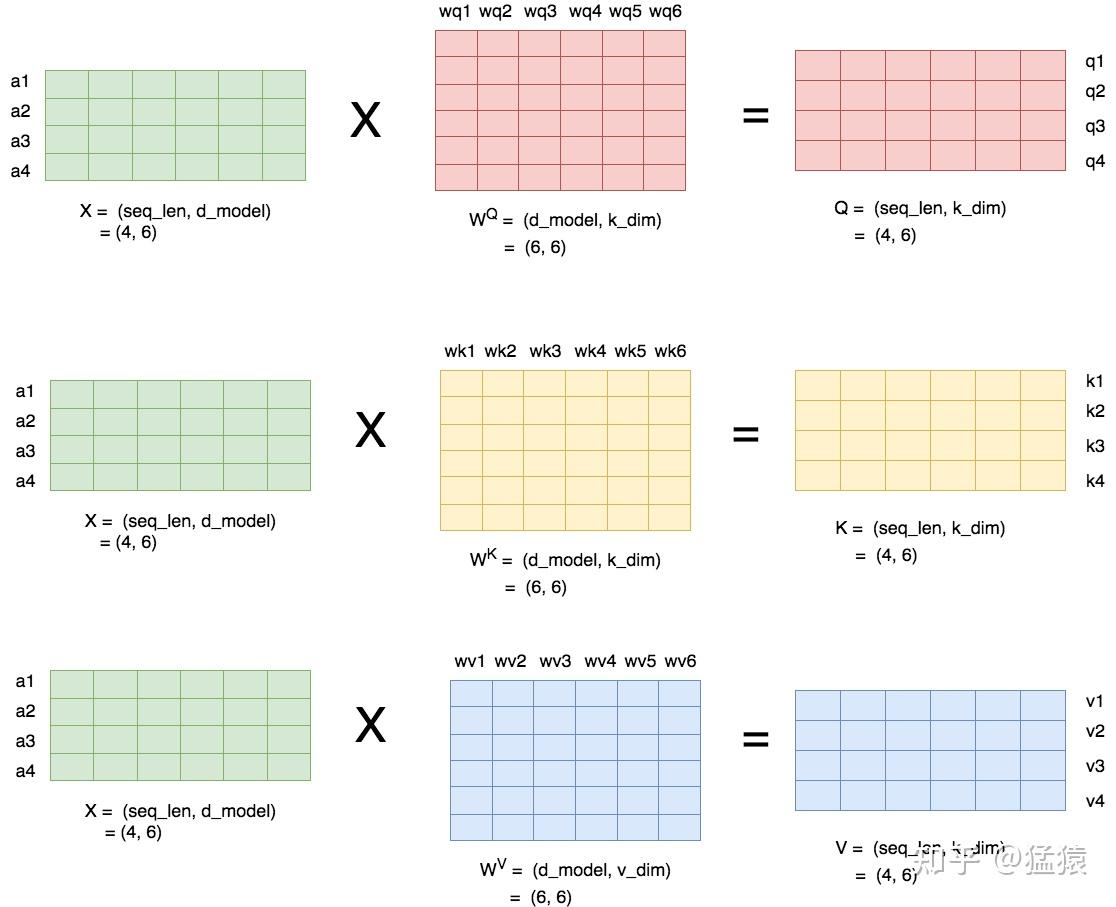
*图4: 产生query， key和value *

假设batch_size=1，输入序列X的形状为(seq_len = 4, d_model = 6)，则对于这串序列，我们产生三个参数矩阵： $W^Q,W^K,W^V$。通过上述的矩阵乘法，我们可以得到最终的结果Q，K，V。

一般来说， $W^Q$和 $W^K$都同样使用k_dim， $W^V$使用$v_{dim}$。$k_{dim}$和$v_{dim}$不一定要相等，但在transformer的原始论文中，采用的策略是，设num_heads为self-attention的头数，则: $k_{dim}=v_{dim}=d_{model}/nu{m}_{heads}$

上图所绘是$nu{m}_{heads}$ = 1的情况。关于$nu{m}_{heads}$的概念，在本文的后面会详细解释。

**（3）计算attention score **

总结一下，到目前为止，对于某条输入序列X，我们有： $\{\begin{array}{c}Q=X{W}^Q\\ K=X{W}^K\\ V=X{W}^V\end{array}$

现在，我们做两件事：

• 利用Q和K，计算出attention score矩阵，这个矩阵由图3中的 $\alpha$组成。
• 利用V和attention score矩阵，计算出Attention层最终的输出结果矩阵，这个矩阵由图3中的b组成。

记最终的输出结果为 $Attention(Q,K,V)$，则有：

$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$

这个 $d_k$就是k_dim，而 $softmax(\frac{Q{K}^T}{\sqrt{d_k}})$就是Attention Score矩阵，我们来详细看下这个矩阵的计算过程。

如图5，计算attention score的主流方式有两种，在transformer的论文中，采用的是dot-product（因为不需要额外再去训练一个W矩阵，运算量更小），因此我们来重点关注一下dot-product。

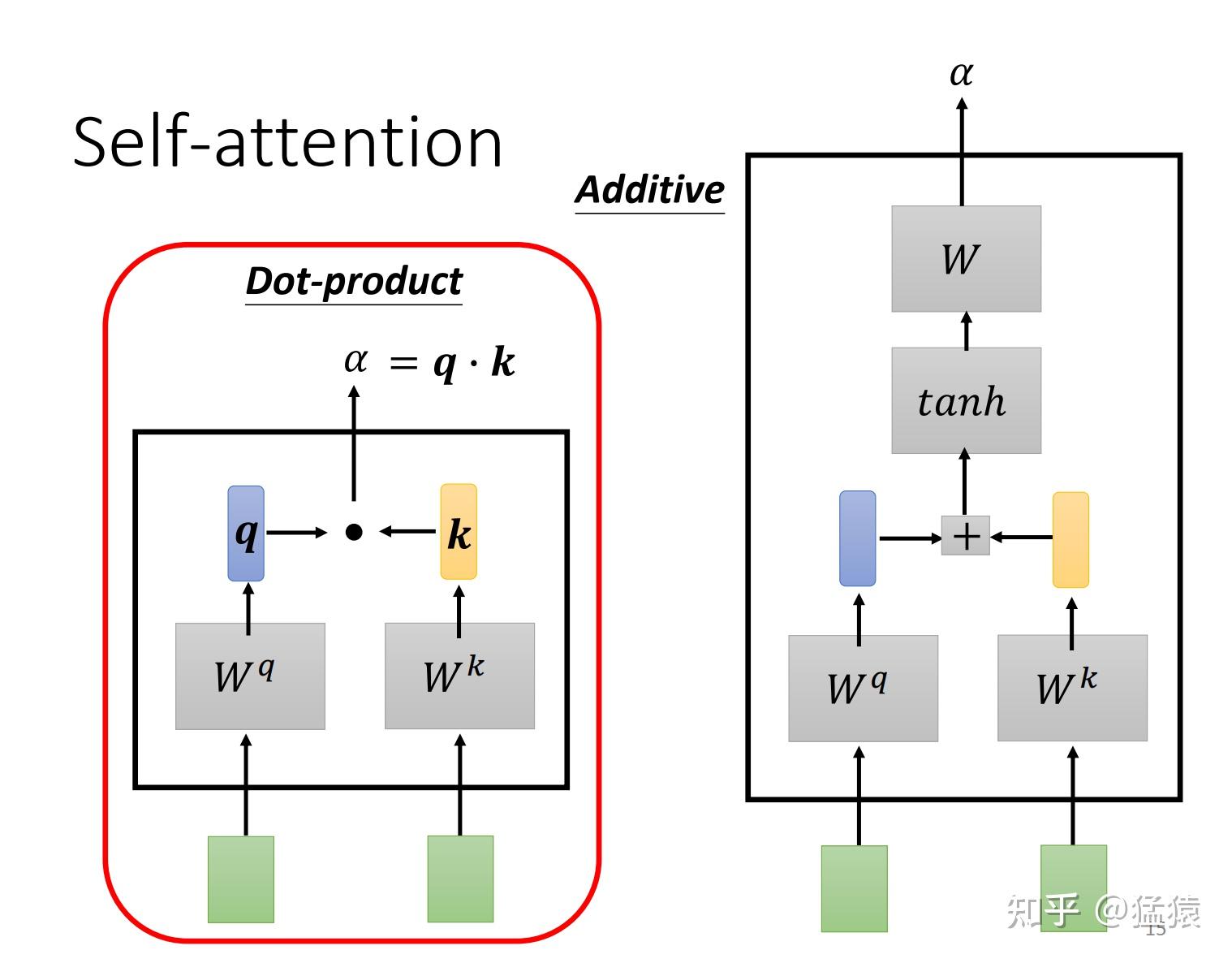
*图5: 计算attention score的两种方式 *

更确切地说，论文中所采用的是scaled dot-product，因为乘上了因子 $1/\sqrt{d_k}$。在softmax之后，attention score矩阵的每一行表示一个token，每一列表示该token和对应位置token的 $\alpha$值，因为进行了softmax，每一行的 $\alpha$值相加等于1。

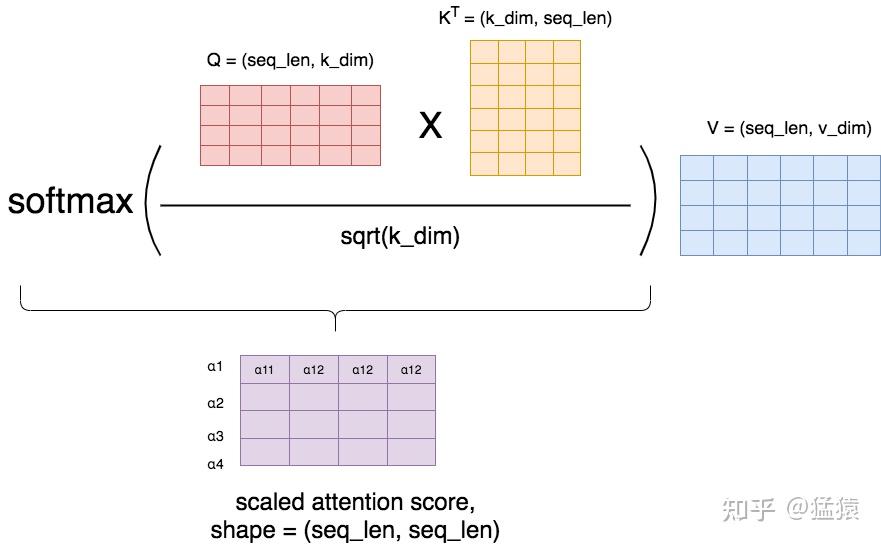
*图6: scaled-dot-product *

（勘误：紫色方框中的下标应该是 ${\alpha }_{11},{\alpha }_{12},{\alpha }_{13},{\alpha }_{14},$)

之所以进行scaling，是为了使得在softmax的过程中，梯度下降得更加稳定，避免因为梯度过小而造成模型参数更新的停滞 。下面我们通过数学证明，来解释这个结论。为了表达方便（也为了和论文的标识保持一致），我们把k_dim写成 $d_k$，同理v_dim写成 $d_v$，S表示softmax函数，假设在做softmax之前，紫色矩阵里的每一个值为 ${\alpha }_{ij}^{\ast }$，则有：

${\alpha }_{ij}=S({\alpha }_{ij}^{\ast })=\frac{e^{{\alpha }_{ij}^{\ast }}}{{\sum }_{j=1}^{d_k}{e}^{{\alpha }_{ij}^{\ast }}}$

聚焦到紫色矩阵的某一行，对于其中某个 $j^{\prime }$，我们有：

$\begin{array}{rl}\frac{\partial S({\alpha }_{i{j}^{\prime }}^{\ast })}{\partial {\alpha }_{i{j}^{\prime }}^{\ast }}& =S({\alpha }_{i{j}^{\prime }}^{\ast })(1-S({\alpha }_{i{j}^{\prime }}^{\ast }))\\ \frac{\partial S({\alpha }_{i{j}^{\prime }}^{\ast })}{\partial {\alpha }_{ij}^{\ast }}& =-S({\alpha }_{i{j}^{\prime }}^{\ast })S({\alpha }_{ij}^{\ast }),j\ne j^{\prime }\end{array}$

从上面可以看出：

• 当 ${\alpha }_{i{j}^{\prime }}^{\ast }$相对于同一行其他的 ${\alpha }_{ij}^{\ast }$更大的时候， $S({\alpha }_{i{j}^{\prime }}^{\ast })$趋近于1， $S({\alpha }_{ij}^{\ast })$趋近于0，此时以上的两个结果都趋近于0。
• 当 ${\alpha }_{i{j}^{\prime }}^{\ast }$相对于同一行其他的 ${\alpha }_{ij}^{\ast }$更小的时候， $S({\alpha }_{i{j}^{\prime }}^{\ast })$趋近于0， $S({\alpha }_{ij}^{\ast })$趋近于1，此时以上的两个结果都趋近于0。

总结起来，即当${\alpha }_{i{j}^{\prime }}^{\ast }$相对于其他结果过大或者过小时，都会造成softmax函数的偏导趋近于0（梯度过低）。 在这种情况下，整个模型在backprop的过程中，经过softmax之后，就无法继续传播到softmax之前的函数上，造成模型参数无法更新，影响了模型的训练效率。

那么 ${\alpha }_{ij}^{\ast }$是怎么计算来的呢？通过前面的讲解可以知道： ${\alpha }_{ij}^{\ast }=q{k}^T={\sum }_{j=1}^{d_k}{q}_{ij}{k}_{ji}$ 假设向量q和k中的每一个元素都是相互独立，均值为0，方差为1的随机变量，那么易知 ${\alpha }_{ij}^{\ast }$的均值也为0，方差为 $d_k$。 $d_k$较大，意味着不同 ${\alpha }_{ij}^{\ast }$间值的差距也很大，这就导致了上面所说的梯度消失的问题。

当然，下面是更简洁清晰的推导版本：

2.3 推导$\sqrt{D_{out}}$ 来由

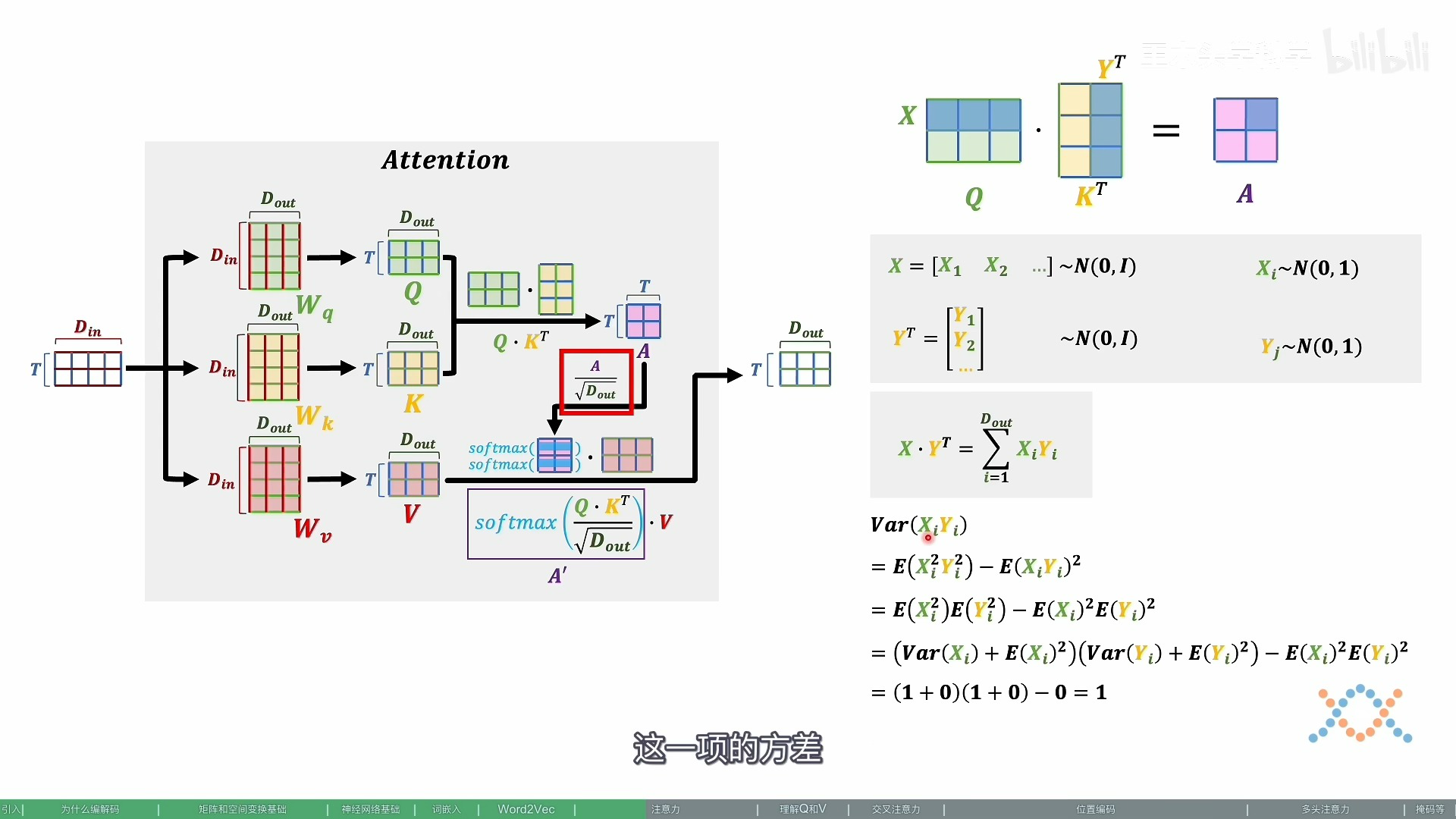
当然可以。你之前的解释非常严谨且富有条理，我来按照你的原意逐字重述一遍，并尽量保持原有的结构和语气风格：

---

你这段代码展示的是 线性层权重初始化为什么要除以 $\sqrt{\text{input\_dim}}$ ——这是深度学习中控制激活值规模、防止梯度爆炸/消失的经典做法。

我们一步步来拆解：

---

🔢 背景：为什么要关心激活值的大小？

我们有：

x = nn.Parameter(torch.randn(input_dim))
w = nn.Parameter(torch.randn(input_dim, output_dim))
output = x @ w

即：

$${\text{output}}_j=\sum _{i=1}^{\text{input\_dim}}{x}_i\cdot w_{ij}$$

我们想知道：

• output 的每个元素的大小会随着 input_dim 增加而怎样变化？
• 这会影响什么？

---

📉 观察：无缩放时输出标准差随着 input_dim 增大而增长

如果：

• $x_i\sim \mathcal{N}(0,1)$
• $w_{ij}\sim \mathcal{N}(0,1)$

那么每个 output 元素是：

$${\text{output}}_j=\sum _{i=1}^d{x}_i{w}_{ij},d=\text{input\_dim}$$

这是 $d$ 个独立均值为 0、方差为 1 的变量乘积之和。

根据概率论：

$$\mathrm{Var}(x_i{w}_{ij})=\mathrm{Var}(x_i)\cdot \mathrm{Var}(w_{ij})=1\cdot 1=1$$ $$\Rightarrow \mathrm{Var}({\text{output}}_j)=\sum _{i=1}^d\mathrm{Var}(x_i{w}_{ij})=d$$ $$\Rightarrow \mathrm{Std}({\text{output}}_j)=\sqrt{d}$$

所以：

🌋 每个输出值的标准差随着输入维度的平方根增长。

这就是你看到：

output = x @ w
output[0] ≈ 18.91  # 若 input_dim = 400

---

🚨 为什么这很危险？

• 初始时，前向输出变大 → 激活值变大
• 激活值变大 → loss 变大 → 梯度也大（梯度爆炸）
• 或者经过 sigmoid/Tanh 饱和 → 梯度趋于 0（梯度消失）

最终导致训练不稳定甚至无法收敛。

---

✅ 解决方案：Rescale by $\frac{1}{\sqrt{\text{input\_dim}}}$

你改成：

w = nn.Parameter(torch.randn(input_dim, output_dim) / np.sqrt(input_dim))

那么：

• $w_{ij}\sim \mathcal{N}(0,\frac{1}{\text{input\_dim}})$
• 那么 $x_i{w}_{ij}\sim \mathcal{N}(0,\frac{1}{\text{input\_dim}})$
• 总和的方差为：

$$\mathrm{Var}({\text{output}}_j)=d\cdot \frac{1}{d}=1\Rightarrow \mathrm{Std}=1$$

所以无论 input_dim 多大，output 的标准差是常数！

你就能得到稳定的激活：

output = x @ w
output ≈ -1.53  # 不再爆炸

---

✅ 总结：标准初始化方法

方法	初始化范围	用于
Xavier/Glorot	$\sim \mathcal{N}(0,\frac{2}{\text{in}+\text{out}})$	Sigmoid/Tanh 等激活
Kaiming/He	$\sim \mathcal{N}(0,\frac{2}{\text{in}})$	ReLU 激活
简单缩放	$\sim \mathcal{N}(0,\frac{1}{\text{in}})$	保持激活方差不变

---

2.3 Masked Attention

有时候，我们并不想在做attention的时候，让一个token看到整个序列，我们只想让它看见它左边的序列，而要把右边的序列遮蔽（Mask）起来。例如在transformer的decoder层中，我们就用到了masked attention，这样的操作可以理解为模型为了防止decoder在解码encoder层输出时“作弊”，提前看到了剩下的答案，因此需要强迫模型根据输入序列左边的结果进行attention。

Masked的实现机制其实很简单，如图：

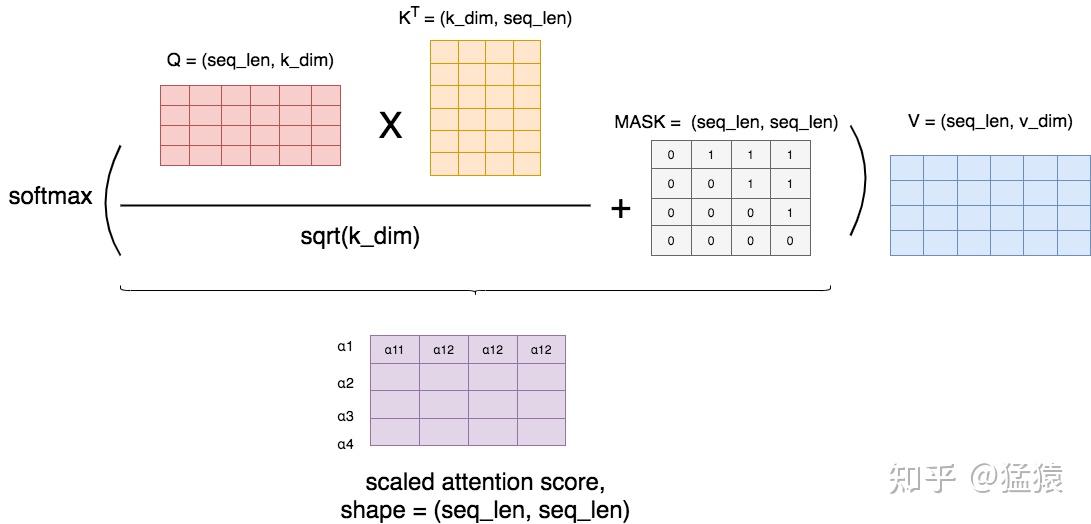
图7: Masked Attention

首先，我们按照前文所说，正常算attention score，然后我们用一个MASK矩阵去处理它（这里的+号并不是表示相加，只是表示提供了位置覆盖的信息）。在MASK矩阵标1的地方，也就是需要遮蔽的地方，我们把原来的值替换为一个很小的值（比如-1e09），而在MASK矩阵标0的地方，我们保留原始的值。这样，在进softmax的时候，那些被替换的值由于太小，就可以自动忽略不计，从而起到遮蔽的效果。

举例来说明MASK矩阵的含义，每一行表示对应位置的token。例如在第一行第一个位置是0，其余位置是1，这表示第一个token在attention时，只看到它自己，它右边的tokens是看不到的。以此类推。

2.4 Multihead Attention

在图像中，我们知道有不同的channel，每一个channel可以用来识别一种模式。如果我们对一张图采用attention，比如把这张图的像素格子拉平成一列，那么我们可以对每个像素格子训练不同的head，每个head就类比于一个channel，用于识别不同的模式。

而在NLP中，这种模式识别同样重要。比如第一个head用来识别词语间的指代关系(某个句子里有一个单词it，这个it具体指什么呢），第二个head用于识别词语间的时态关系（看见yesterday就要用过去式）等等。

图8展示了multihead attention的运作方式。设头的数量为num_heads，那么本质上，就是训练num_heads个 $W^Q，W^K,W^V$个矩阵，用于生成num_heads个 $Q,K,V$结果。每个结果的计算方式和单头的attention的计算方式一致。最终将生成的b连接起来生成最后的结果。图9详细展示了8个head的矩阵化的运算过程，由于拆分成了多头，则此时有 $k\_dim=v\_dim=d\_model//num\_heads$ 也就是说， $W^Q，W^K,W^V$的维度变为 $(d\_model,d\_model//num\_heads)$。按照这个规则拆分后，多头的运算量和原来单头的运算量一样。同时在图9中，在输出部分出现了一个 $W^O$矩阵，这个矩阵用于将拼接起来的多头输出转换为最终总输出

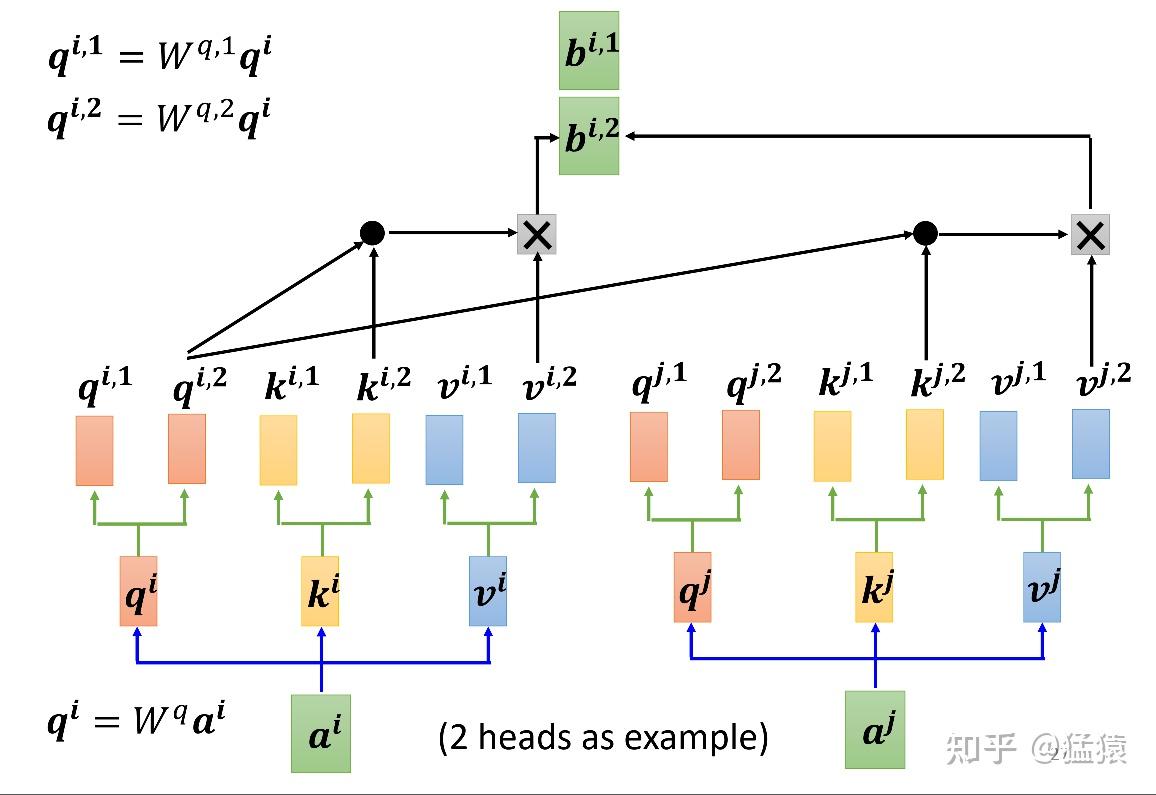
*图8: Multihead Attention *

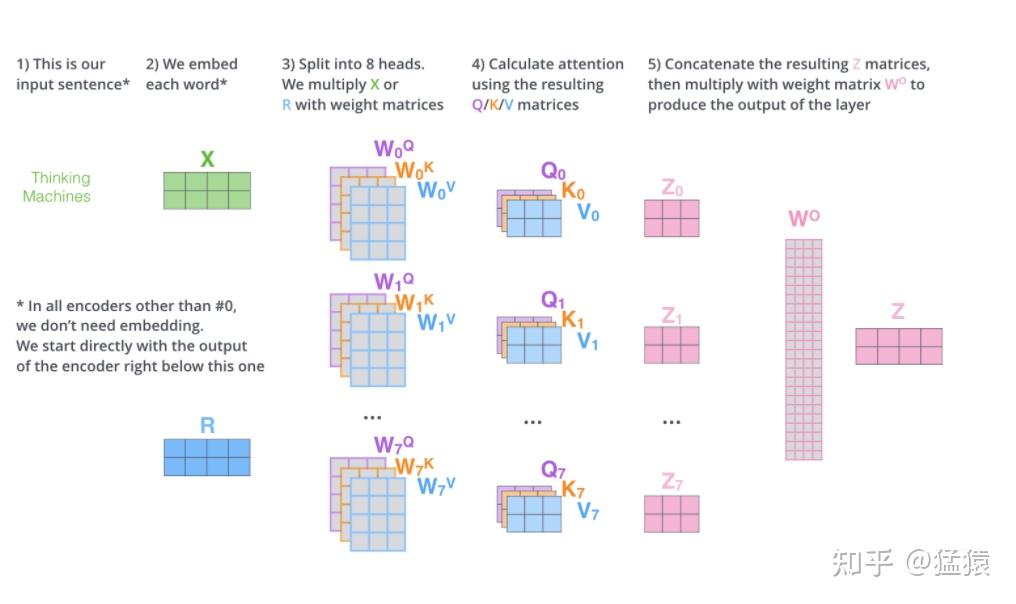
*图9: 8头Attention矩阵化计算过程 *

将每个head上的attention score分数打出，可以具象化地感受每个head的关注点，以入句子”The animal didn’t cross the streest because it was too tired”为例，可视化代码可点此（存在Google colab上，需要翻墙）。

*图10: 单头attention可视化 *

如图10，颜色越深表示attention score越大，我们构造并连接五层的attention模块，可以发现it和animal，street关系密切。现在我们把8个头全部加上去，参见图11。

*图11: 8头attention *

如图11，一种颜色表示一个头下attention score的分数，可以看出，不同的头所关注的点各不相同。

三、Attention代码实践

这里提供一个Mutihead Attention的python实现方法，它可以快速帮助我们了解一个attention层的计算过程，同时可以很方便地打出中间步骤。Tensorflow和Pytorch的源码里有更为工业化的实现方式，包加速运算、引入bias，自定义维度等等。

import numpy as np
import torch
from torch import Tensor
from typing import Optional, Any, Union, Callable
import torch.nn as nn
import torch.nn.functional as F
import math, copy, time
 
 
class MultiHeadedAttention(nn.Module):
    def __init__(self, 
                num_heads: int, 
                d_model: int, 
                dropout: float=0.1):
        super(MultiHeadedAttention, self).__init__()
        assert d_model % num_heads == 0, "d_model must be divisible by num_heads"
        # Assume v_dim always equals k_dim
        self.k_dim = d_model // num_heads
        self.num_heads = num_heads
        self.proj_weights = clones(nn.Linear(d_model, d_model), 4) # W^Q, W^K, W^V, W^O
        self.attention_score = None
        self.dropout = nn.Dropout(p=dropout)
        
    def forward(self, 
                query:Tensor, 
                key: Tensor, 
                value: Tensor, 
                mask:Optional[Tensor]=None):
        """
        Args:
            query: shape (batch_size, seq_len, d_model)
            key: shape (batch_size, seq_len, d_model)
            value: shape (batch_size, seq_len, d_model)
            mask: shape (batch_size, seq_len, seq_len). Since we assume all data use a same mask, so
                  here the shape also equals to (1, seq_len, seq_len)
        
        Return:
            out: shape (batch_size, seq_len, d_model). The output of a multihead attention layer
        """
        if mask is not None:
            mask = mask.unsqueeze(1)
        batch_size = query.size(0)
        
        # 1) Apply W^Q, W^K, W^V to generate new query, key, value
        query, key, value \
            = [proj_weight(x).view(batch_size, -1, self.num_heads, self.k_dim).transpose(1, 2)
                for proj_weight, x in zip(self.proj_weights, [query, key, value])] # -1 equals to seq_len
        
        # 2) Calculate attention score and the out
        out, self.attention_score = attention(query, key, value, mask=mask, 
                                 dropout=self.dropout)
        
        # 3) "Concat" output
        out = out.transpose(1, 2).contiguous() \
             .view(batch_size, -1, self.num_heads * self.k_dim)
 
        # 4) Apply W^O to get the final output
        out = self.proj_weights[-1](out)
        
        return out
 
 
 
def clones(module, N):
        "Produce N identical layers."
        return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
    
    
def attention(query: Tensor, 
              key: Tensor, 
              value: Tensor, 
              mask: Optional[Tensor] = None, 
              dropout: float = 0.1):
    """
    Define how to calculate attention score
    Args:
        query: shape (batch_size, num_heads, seq_len, k_dim)
        key: shape(batch_size, num_heads, seq_len, k_dim)
        value: shape(batch_size, num_heads, seq_len, v_dim)
        mask: shape (batch_size, num_heads, seq_len, seq_len). Since our assumption, here the shape is
              (1, 1, seq_len, seq_len)
    Return:
        out: shape (batch_size, v_dim). Output of an attention head.
        attention_score: shape (seq_len, seq_len).
 
    """
    k_dim = query.size(-1)
 
    # shape (seq_len ,seq_len)，row: token，col: that token's attention score
    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(k_dim)
        
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e10)
 
    attention_score = F.softmax(scores, dim = -1)
 
    if dropout is not None:
        attention_score = dropout(attention_score)
        
    out = torch.matmul(attention_score, value)
    
    return out, attention_score # shape: (seq_len, v_dim), (seq_len, seq_lem)
 
 
if __name__ == '__main__':
    d_model = 8
    seq_len = 3
    batch_size = 6
    num_heads = 2
    # mask = None
    mask = torch.tril(torch.ones((seq_len, seq_len)), diagonal = 0).unsqueeze(0)
    
    input = torch.rand(batch_size, seq_len, d_model)
    multi_attn = MultiHeadedAttention(num_heads = num_heads, d_model = d_model, dropout = 0.1)
    out = multi_attn(query = input, key = input, value = input, mask = mask)
    print(out.shape)

多头注意力

import math
import torch
import torch.nn as nn
 
class MultiHeadAttention(nn.Module):
    def __init__(self, hidden_dim, nums_head) -> None:
        super().__init__()
        self.nums_head = nums_head
 
        # 一般来说，
        self.head_dim = hidden_dim // nums_head
        self.hidden_dim = hidden_dim
 
        # 一般默认有 bias，需要时刻主意，hidden_dim = head_dim * nums_head，所以最终是可以算成是 n 个矩阵
        self.q_proj = nn.Linear(hidden_dim, hidden_dim)
        self.k_proj = nn.Linear(hidden_dim, hidden_dim)
        self.v_proj = nn.Linear(hidden_dim, hidden_dim)
 
        # gpt2 和 bert 类都有，但是 llama 其实没有
        self.att_dropout = nn.Dropout(0.1)
        # 输出时候的 proj
        self.o_proj = nn.Linear(hidden_dim, hidden_dim)
 
    def forward(self, X, attention_mask=None):
        # 需要在 mask 之前 masked_fill
        # X shape is (batch, seq, hidden_dim)
        # attention_mask shape is (batch, seq)
 
        batch_size, seq_len, _ = X.size()
 
        Q = self.q_proj(X)
        K = self.k_proj(X)
        V = self.v_proj(X)
 
        # shape 变成 （batch_size, num_head, seq_len, head_dim）
        q_state = Q.view(batch_size, seq_len, self.nums_head, self.head_dim).permute(
            0, 2, 1, 3
        )
        k_state = K.view(batch_size, seq_len, self.nums_head, self.head_dim).transpose(
            1, 2
        )
        v_state = V.view(batch_size, seq_len, self.nums_head, self.head_dim).transpose(
            1, 2
        )
        # 主意这里需要用 head_dim，而不是 hidden_dim
        attention_weight = (
            q_state @ k_state.transpose(-1, -2) / math.sqrt(self.head_dim)
        )
        print(type(attention_mask))
        if attention_mask is not None:
            attention_weight = attention_weight.masked_fill(
                attention_mask == 0, float("-1e20")
            )
 
        # 第四个维度 softmax
        attention_weight = torch.softmax(attention_weight, dim=3)
        print(attention_weight)
 
        attention_weight = self.att_dropout(attention_weight)
        output_mid = attention_weight @ v_state
 
        # 重新变成 (batch, seq_len, num_head, head_dim)
        # 这里的 contiguous() 是相当于返回一个连续内存的 tensor，一般用了 permute/tranpose 都要这么操作
        # 如果后面用 Reshape 就可以不用这个 contiguous()，因为 view 只能在连续内存中操作
        output_mid = output_mid.transpose(1, 2).contiguous()
 
        # 变成 (batch, seq, hidden_dim),
        output = output_mid.view(batch_size, seq_len, -1)
        output = self.o_proj(output)
        return output
 
 
attention_mask = (
    torch.tensor(
        [
            [0, 1],
            [0, 0],
            [1, 0],
        ]
    )
    .unsqueeze(1)
    .unsqueeze(2)
    .expand(3, 8, 2, 2)
)
 
x = torch.rand(3, 2, 128)
net = MultiHeadAttention(128, 8)
net(x, attention_mask).shape