图像数据具有二维信息结构,深度信念网络(DBN)仅对数据进行了一维向量化,没有充分结合二维数据结构特点。卷积神经网络(Convolutional Neural Network, CNN)的工作原理受哺乳动物视觉过程的启发,架构上更接近生物学意义上的神经网络,更适合处理二维的图像数据,在人脸识别、医疗影像和无人驾驶等计算机视觉领域应用广泛,是推动深度学习迅速发展最主要的动力之一。可以将CNN看成是多层感知器(MLP)的变型,使用局部连接替代了MLP的全联接。
1. 历史及应用
1979年,日本学者福岛邦彦(Kunihiko Fukushima)[1]提出了通过学习的方法,建立了视觉识别模式的多层架构Neocognitron,将感知野 (Receptive Field)概念引入了人工神经网络领域,这可以说是卷积神经网络(CNN)的鼻祖。
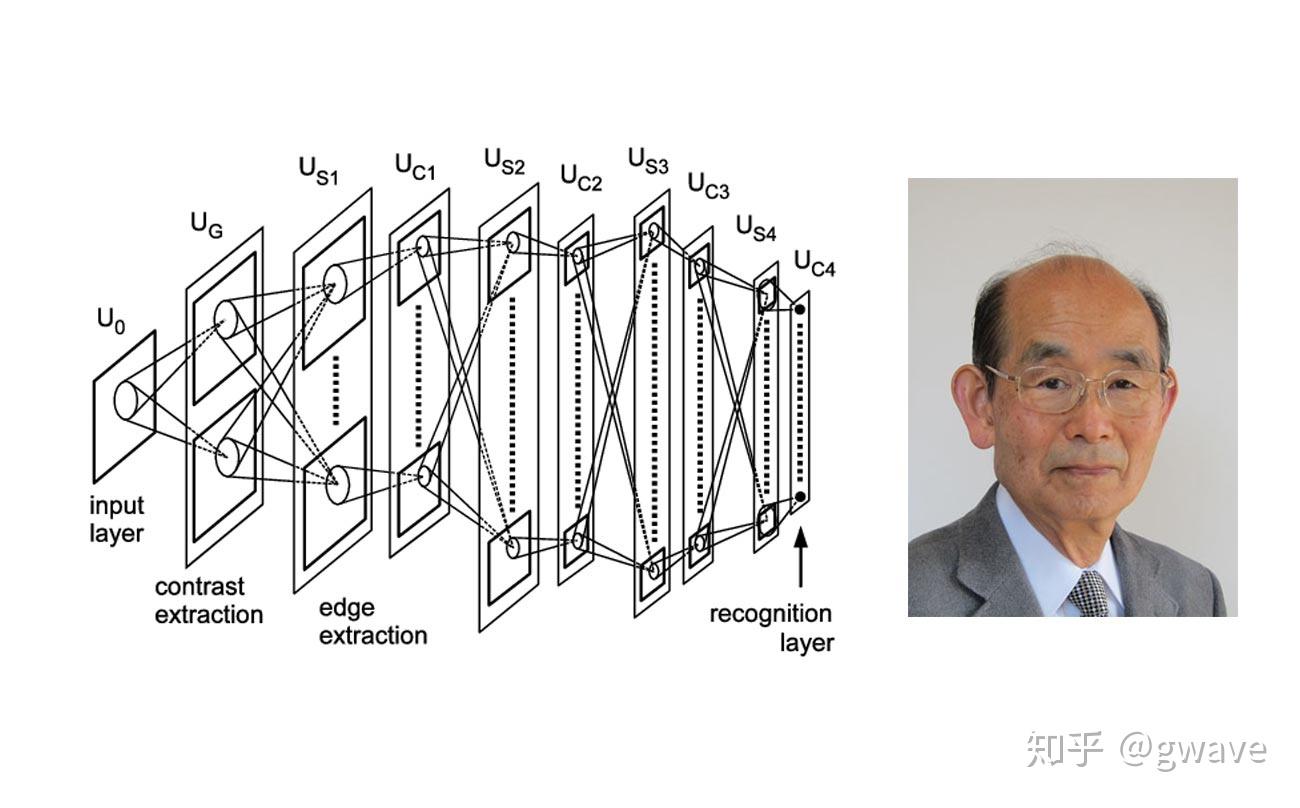
1998年杨立昆(Yann LeCun)和尤舒·本吉奥(Yoshua Bengio)等在前人的基础上进行了改进,研发了著名的神经网络LeNet-5,成功地识别出手写数字,并被商业化应用于手写支票的识别,但受数据、计算资源等多方面局限,在处理更复杂的问题时,遇到较多困难,没能全面普及。他们两人和Hinton一起获得了2019年图灵奖。
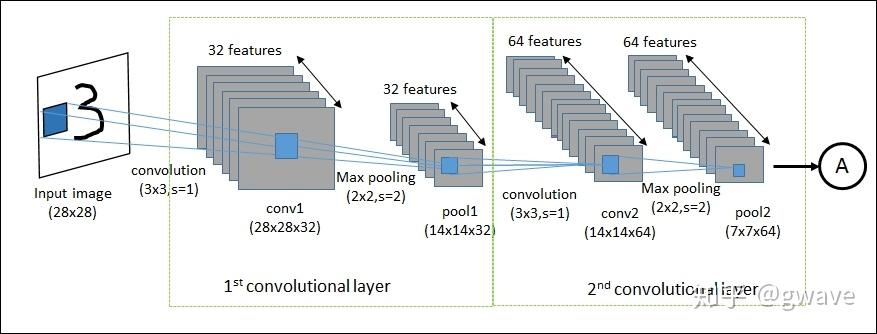
LeNet-5
2012年,在基于混合国家标准与技术学院(Mixed National Institute of Standard and Technology, MNIST)数据库[2]的图像识别中,CNN创造了历史记录,错误率仅为0.23%[[iii]],可与人媲美。同年,辛顿教授与学生Alex Krizhevsky等人使用CNN(AlexNet)架构在ImageNet[3]的竞赛中获得冠军,错误率仅为16.4%,大幅领先于第二名26.2%,随后,谷歌斥巨资收购了他们的创立的仅数月的深度学习公司DNNresearch,由此CNN引爆了机器学习领域,引起了工业界和学术界的广泛重视,大量基于CNN的商业化应用与创新涌现出来,直接推动了AI的第三次繁荣。
近年来,CNN在图像识别、视频分析、声音识别、自然语言处理等领域取得了巨大的突破,甚至被应用于围棋博弈之中,2016年3月,采用了13层CNN的谷歌AlphaGo以4:1击败了拥有过16个世界冠军头衔的李世石九段,2017年5月,升级到40层CNN的AlphaGo 2.0以3:0击败了世界排名第一的柯洁九段,CNN的本质在于抽象,这也同样是围棋的精髓。在工业界,互联网巨头们和创业公司也纷纷将CNN作为重点研究方向,CNN也走出了计算机视觉的领域,在金融领域,CNN被用来进行基于时间序列的股价预测和算法交易;在电商/零售行业,CNN被用来重新定义客户与品牌的关系,包括客户的商品浏览方式和购买决定的分析;在医疗领域,CNN对肺癌进行筛查的准确率已远超过医生。
2. 降维利器:局部感知与权重共享
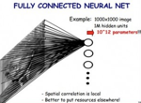
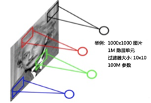
在图像识别领域,假设一张(黑白)照片的分辨率为1000×1000,像素数量为一百万,每个像素对应一个特征,就有 个特征。对于SVM和逻辑回归等传统的机器学习算法而言,要训练这么多参数,所需的数据量将极为庞大,高维度特征引起的“维度灾难”使算法难以求解。如果采用人工神经网络多层感知器算法MLP,假设输入层神经元与像素一一对应( ),隐层神经元数量与输入层的神经元数量相同,由于MLP的层与层之间的神经元间采用的是全连接(Fully Connected[4]),所有输入层与隐层的神经元全部互联,这将产生 个权重参数,数量庞大到几乎无法训练。2013年AlexNet只有 个参数,在GPU机器上训练了近1周。
60年代初,约翰霍普金斯大学的休伯儿(Hubel)和威泽尔(Wiesel)对猫视觉机制的研究表明:对视网膜的光照,由光感细胞转化为电脉冲后,输送至大脑视皮层神经元进行处理。单个视皮层神经元仅对视网膜的某特定区域的光刺激敏感,该视网膜区域被称为此神经元所对应的“感知野”。感知野以平铺的方式覆盖整个视野,仅对图像的局部敏感,此特点能有效地降低神经网络的复杂性,并能发现图像中目标间的空间关系。一般认为,大脑对外界的认知模式是从局部到全局,从图像中像素的空间联系来看,通常临近的像素间相关性较高,而距离较远的像素间的相关性较弱。因此,神经网络中的隐层的单一神经元没有必要对图像进行全局感知,而只需感知图像的局部,也就是说:隐层神经元只需连接输入层上局部相关的像素即可,从中提取初级特征,然后在更高层次上,再多次重复该过程,将局部特征信息再进行不断抽象,最终只需感知少量的高级特征的组合即可。
CNN实现了局部感知野 (Local Receptive Field) 的概念:上例中像素数量为 ,如果隐层神经元仅进行局部感知,假设每个隐层神经元仅连接10×10=100个像素(图3-91(a)),那么需要训练的权重数量等于隐层神经元数量 乘以其所连接的像素数量(100),结果为 ,相比全连接的情况,连接数降低了4个数量级,但数量仍然庞大。
隐层神经元的一套权重参数也被称为是一个滤波器(Filter), 通过与图像的卷积能从中检测出特定的特征(比如某角度的线条),滤波器与该图像特征是一一对应的,这与视皮层V1的简单细胞仅对某种特征敏感是类似的(图3-92)。因此,我们再引入一个新的假设:让所有隐层神经元共享权重!这意味着上例中一百万 个隐层神经元都使用同一套权重参数(图3-91(b)),权重参数的数量将再下降一百万倍,即只需 100个参数[5]就够了!卷积神经网络两大核心思想 — 局部感知 和权重共享 大幅降低了数据的维度,这使数据维度与感知野的大小相等,而与像素数量和隐层神经元数量都无关,因为不论隐层神经元数量有多少,都共享一套权重参数,虽然像素数量的增加会导致隐层神经元数量的增加,但并不会导致权重参数的数量增加。


图3-91 (a) 局部感知的神经网络 (b)权重共享的局部感知神经网络 (c) 多滤波器、局部感知和权重共享的神经网络
但是,以上假设所有神经元都共享一套权重的想法将问题过于简化了,事实上,图像中存在多种特征需要被提取,因此,需要多套权重,或者说需要多个滤波器才能实现对不同特征的提取 。假设图像中存在50种特征,因为某种滤波器仅能提取一种相对应的特征(如某特定角度的圆弧边缘),那么就需要50个过滤器(图3-91(c))。每个滤波器的参数不同,处理的特征不同,彼此间相互独立。上面例子中每个特征对应100个权重共享的滤波器参数,那么,50个特征共对应50×100=5000个参数,这样规模权重参数的数量比较适合利用机器学习进行训练的。用滤波器(也称卷积核)对图像进行卷积(Convolution)运算,得到特征映射(Feature Map),基于同一输入图片,50个滤波器会生成50个特征映射,这50个特征映射组成了网络的一个隐层。图3-92(a)显示4个滤波器(水平、垂直与2个左右倾斜45度)通过卷积运算分别检测到并提取了图像中的4种不同的特征,并形成右侧的4个特征映射。图3-92(b)中显示了一个7×7的曲线滤波器,注意到沿着曲线方向的权重为30,而其他位置为0。滤波器的权重可经过训练(BP)获得。
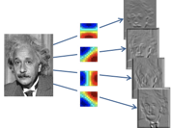

图3-92(a) 多滤波器提取不同的图像特征[6](b) 曲线滤波器
由于特征映射是由与之对应的滤波器所生成的,所以,隐层的(由多个特征映射构成)权重数量与隐层的神经元数量无关,而是等于滤波器的数量×局部感知野的大小(假设不同滤波器大小相同)。然而,隐层的大小则与原图像的像素数、滤波器的大小以及在图像中的滑动步长(Stride)相关,假设先只考虑1个滤波器的情况,上例中图像像素尺寸为1000x1000,滤波器大小为10x10,若滤波器滑动步长为10(下一节将详细介绍),即在没有重叠的情况下,则需要隐层神经元数量为(1,000x1,000)/(10×10)= 10,000个神经元,即横行和纵向各需要滑动100次才能覆盖整张照片,每滑动一次进行一次卷积,对应隐层的一个神经元;若滑动步长为8,那么每次滑动会有两个像素重叠,滤波器的初始位置是[1,10][7],第一次滑动至[9,18],若以n表示滑动步数,那么第n次滑动的滤波器位置为[1+8×n,10+8×n], 需要经过(1000-10)/ 8 次,即124次滑动才能覆盖1000个像素,现有1,000×1,000个像素,所以需要124×124=15,376个隐层神经元才能完全覆盖照片,而这15,376个神经元共享100个权重,这与步长为10的情况完全相同,不同的是隐层神经元数量从10,000增长为15,376。这是一个滤波器的情况,如果有n个滤波器,隐层神经元数量和共享权重的参数数量就都要再乘以n倍。
总之,图像尺寸越大,像素越多,卷积之后对应的隐层神经元数量也越多,但由于所有隐层神经元是共享权重的,所以权重参数的数量并不会因图像越大而增加,而等于滤波器数量与局部感知野大小的乘积,滤波器的数量等于所需要提取的特征数量。
3. 卷积神经网络(CNN)的构件与发展
与其他深度神经网络相同,卷积神经网络(CNN)也是由多层网络结构所组成,通常包含三种类型的网络层:卷积层 、池化层 和全连接层 。
卷积层 一般是个正方形[8]的神经元网格,下图中:卷积层的输入是前层(例如输入层)的神经元网格(左侧5×5绿色方阵),卷积运算输出的结果是右侧3×3方阵。局部感知的滤波器(右下角的3×3橙色方阵)是一个滑动窗口,也称为卷积核 (Kernel),从左向右,从上向下滑动,将卷积核覆盖的输入值与权重进行卷积,右下角的九宫格表示的是卷积核滑动到最右侧和最下方的情况,这与右侧卷积输出矩阵中右下角4相对应。以步长为1上下左右来滑动滤波器,就能计算出右侧3×3矩阵的9个值的所有输出。卷积层的功能类似视觉皮层中的简单细胞,用于局部特征检测。
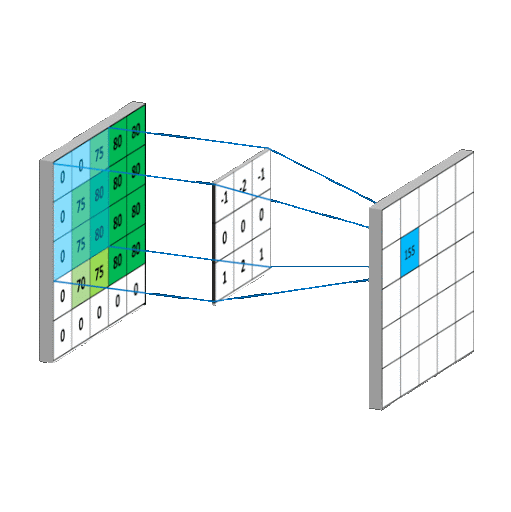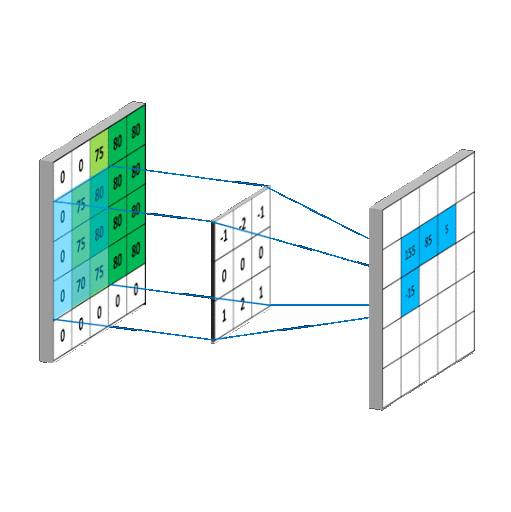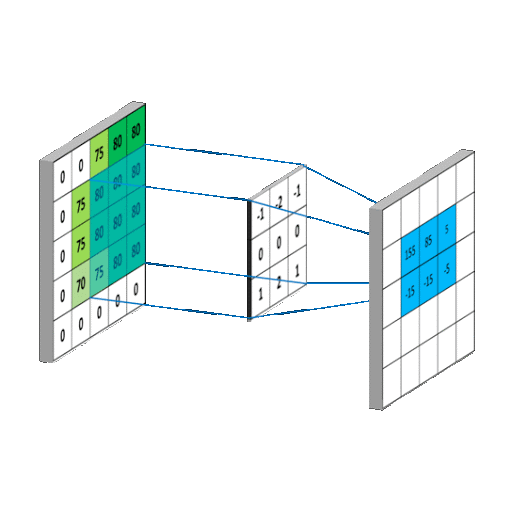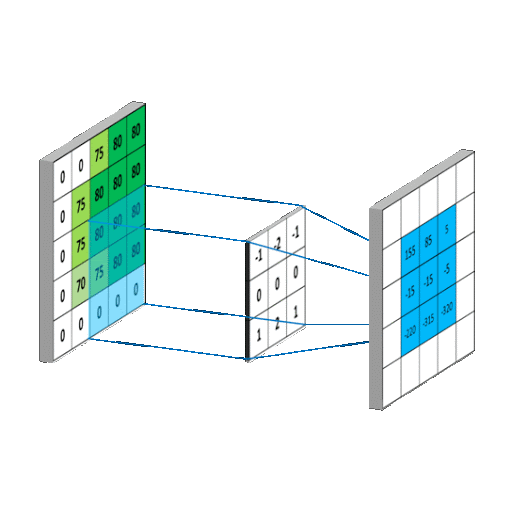
卷积过程
在通过卷积核提取了特征后,很自然的我们希望利用这些特征来进行分类。在卷积过程中,如果步长等于2,得到的特征映射大小会约[9]是输入的1/4,步长越大信息损失也越大,因此,一般情况下设定卷积核滑动的步长等于1,这样卷积前后的图像尺寸基本不变,假设有n个过滤器,隐层神经元数量就是n倍特征映射的大小,最终分类算法的输入参数的数量仍然太多而难以处理,需要进一步降维。
在CNN中,常用的降维方法是在卷积层之间加入池化层 (Polling Layer)。池化层的目的是在保留有效信息的前提下,减少数据量和计算量,并降低过拟合 的风险[10]。池化层对卷积层输出的矩阵进行下采样 (subsampling),产生输出。如图3-94中,对左侧4×4矩阵,以2×2的过滤器进行最大值池化(Max Pooling),从2×2的过滤器矩阵中选出最大值作为单个输出,构建右侧新的采样层,最大值池化倾向于将卷积所发现的特征保留下来,同样保留该特征与其他特征的相对位置关系。除了最大值池化之外,均值池化也常见 ,但有将图像模糊化的趋势。
卷积层与尾随的池化层所形成的对偶结构与动物大脑视皮层结构是类似的:卷积层与池化层分别对应简单细胞和复杂细胞,简单细胞后紧跟着复杂细胞,池化层对卷积层输出的局部特征进行筛选,仅保存重要信息。

图3-94 最大值 v.s. 平均值采样 来源:http://deeplearning.cs.cmu.edu/notes/CNN2.pdf

CNN整个深度架构中常存在由多个由卷积层和采样层组合而成的层,图3-95[11]所示的是经典的手写数字识别的LeNet-5, 分为Layer 1和Layer 2[[iv]]两层。卷积与池化过程如下:
-
输入图像尺寸为32×32;
-
C1层有6个滤波器提取不同的特征,形成6个特征映射(28×28),每个特征映射内部的权重是共享的。滤波器的尺寸为5×5(图上未标注),在图像上作水平/垂直的滑动,滑动步长为1。每个滤波器有5×5=25个参数,加上1个偏置(Bias)参数,共26个,6个滤波器共有26×6=156个参数。
-
S1是对C1进行池化得到的结果,特征映射的数量保持不变,仍是6个, 特征平面的长宽减半为14×14,S1的每个神经元与C1中的4(2×2)个相邻神经元相对应(参考图3-94)。
-
C2层是对S1层的卷积,方法与C1相同,在长宽均为14的S2上,以步长为1滑动尺寸为5×5的的过滤器,共移动10次,即可完全覆盖14个神经元;不同点在于S2 并不是只有1层,所以C2与S1间的连接需要按照一定顺序[12]进行组合,共16种组合,于是C2由16个10×10的平面组成;
-
对C2层进行池化,得到由16个5×5单元所组成得采样层S2;
-
F3是一个由120 个特征映射所组成的卷积层。由于S2已经与滤波器的大小相同,均为5×5,所以滤波器的窗口已无需滑动,F3的特征映射的大小是1×1,这导致了F3与S2之间的实质上的全连接。
-
F3到(10个数字分类)的输出层之间是全连接。
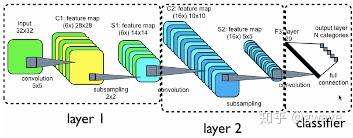
图3-95 CNN卷积层与采样层的组合
全连接层 (Fully-Connected Layer,FC Layer)通常位于数个卷积层/采样层的组合之后[13],在整个CNN架构的末端位置,也称稠密层(Dense Layer),其作用相当于一个普通的分类器。全连接层的结构与多层感知器相同,不同层的神经元之间完全连接,所以,连接的参数量很大,容易受到过拟合的困扰。
辛顿教授有句名言:“你还没有过拟合的原因是网络还不够大”。当神经网络深度越来越深,规模越来越大时,过拟合的风险就会明显上升。 近年来,Dropout一种被普遍应用的防止过拟合的方法,它在模型训练过程中,随机忽略一定比例隐层节点(50%是个不错的初始值),能有效防止过拟合(图3-96)。Dropout背后的逻辑是:如果一个神经元了解它与哪些其他神经元存在连接,在训练过程中,神经元之间会相互适应和调整以“合谋”以获得“更好”的表现,这加剧了过拟合的发生。隐层神经元如果要与其他神经元良好地合作,它需要能独立地做些既有用又不同于其他神经元的事情。
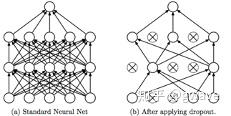
图3-96 标准的神经网络与经过Dropout之后的对比 图3-97 ReLU与Softplus
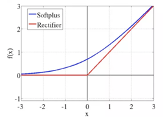
CNN经常使用小批量梯度下降(Mini-Batch)来训练模型,在选择非线性变换的函数时,过去常使用Sigmoid函数作为激活函数[14],由于Sigmoid函数比较平缓,最大的梯度位于0附近,也大约只有1/4左右,也就是每经过一层反向传播,至少要损失3/4的梯度,当网络层数多了之后,“梯度消失”问题就会很严重。2012年以来,线性整流单元ReLU[15](Rectifier Linear Units)已成为神经网络中应用最广泛的激活函数,它计算性能优良(如果x⇐0, y=0 ; x >0, y=x)(图3-97)。有学者认为,ReLU比Sigmoid函数更具有生物学合理性。
ReLU、Dropout和最大池化是辛顿教授与他的学生 Alex Krizhevsky在2012年ImageNet 挑战赛中率先引入CNN的,将识别错误率大幅降低到16.4%,远远领先于第2名(SVM)26.2%的错误率,他们也率先使用GPU训练模型,大幅度提升了训练效率,AlexNet 共有65万个神经元,6000万个参数,5个卷积/池化层,3个全连接层, 最后一层是处理1000个类别的SoftMax(图3-98) 。AlexNet的惊人表现引起了对CNN的广泛关注,ImageNet挑战赛也成了深度学习和AI进展的标杆。
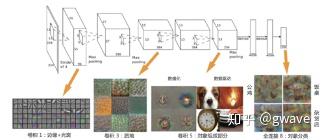
图3-98 AlexNet 8层CNN架构 (2012)
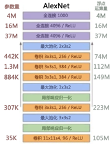
2014年ImageNet的冠军是GoogLeNet ,据说名称中大写的“L”是为了向Yann LeCun的 LeNet致敬。GoogLeNet 也被称为Inception V1[16](图3-99), 参数量只有500万,大约只有AlexNet的1/12,但是获得了更好的表现,Top-5的误差率只有6.67%, 还不到AlexNet的一半。Inception V1的深度达22层,比8层的AlexNet结构上要深的多,也比同年的另一个优秀模型VGGNet的19层要更深,但是计算量却控制在15亿次浮点计算,的确属于非常优秀和实用的模型。
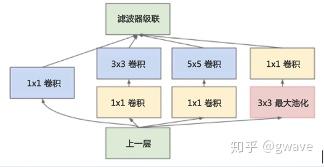
图3-99 Inception模块 (2014)
Inception V1参数少效果好的原因除了模型深度达、表达能力更强外,还有两点创新:
§ 对于同一输入图像,使用不同结构与尺寸的卷积和进行特征提取操作,然后把的到的结果进行串联,使不同的特征“融合”。
§ 去除了CNN末端的全连接层,以全局平均池化层来取代它[17]。
Inception V1的论文中指出,Inception Module可以让网络的深度和宽度高效率地扩充,提升准确率且不致于过拟合。在之后继续发表的论文中,Inception的结构被不断改进,在最新版本Inception V4中,作者尝试与另一种新网络结构—残差网络(ResNet)进行相结合,充分发挥两种结构的优点,获得更好的图像识别的能力。
2015年ImageNet挑战赛冠军由微软亚洲研究院He Kaiming等人提出的深度残差网络 (ResNet)获得,其深度达到了破纪录的152层(实验达到1202层,效果也不错),错误率进一步下降到了3.57%,参数量小于VGGNet,效果非常突出。残差网络之所以能横扫天下,主要是它解决了一个深度学习中的一个至关重要的问题:网络深度。自AlexNet石破天惊的把识别误差率腰斩之后,计算机视觉领域的科学家们都意识到神经网络的层数对于深度模型是至关重要的,神经网络越深,表达力越强,模型表现就可能越好,但是随之而来的是训练难度增大,因为“梯度消失/爆炸”的问题会随着网络层数的增加而加重 ,批正则化(Batch Normalization,BN)[18]、初始化权重正则化、使用ReLU作为激活函数等创新在一定程度上缓解了这个问题,使网络深度增加到了20层左右,但再进一步增加网络深度,模型会发生退化(Degradation),无论如何调参,50层的网络的训练和测试误差总是高于20层网络的误差,梯度消失/爆炸的问题并没有被彻底解决,残差网络的提出正是为了解决这个问题。
在残差网络被发明之前,另一位深度学习泰斗Juergen Schmidhuber[19]教授提出了高速公路网络 (Highway Network),ResNet的思想与之有相通之处。高速公路网络的目标就是解决梯度消失的问题,此前我们提到的所有激活函数(如Sigmoid)都是对输入进行非线性变换,高速公路网络相当于改变了每一层的激活函数,它保留了一定比例的原始输入,不经过非线性变换直接输入下一层,因此,梯度不会损失,仿佛一条信息高速公路,高速公路网络也因此而得名。
多层感知器(MLP)与大部分机器学习算法(如逻辑回归、决策树和SVM等)均属于判别模型(Discriminative Model),如图3-100(a)所示,它们利用输入数据 和标签 来构建一个函数 ,也就是直接从数据 中学习 。残差网络与高速公路网络非常类似, 残差网络使用全等映射(Identity Mapping)使前一层的输入 直达输出端。如图3-100(b)所示: 是输入; 是从输入到输出的映射函数,就是一般情况下判别模型的所要拟合的目标函数;由于在残差模型中 被直接接入输出端,所以 ,待学习的目标也就变成了残差函数 。 是输出相对于输入 的变化,被称为残差,这也是残差网络名字的由来。
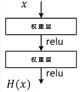
图3-100(a) MLP等判别模型 图3-100(b) ResNet的残差学习单元
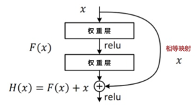
ResNet的三个特性:
-
由于短路连接,在梯度反向传播时,不会出现梯度消失的情况;
-
全等映射直接接通了网络某几层的输入和输出,与电路中的短路类似。如果网络的深度很大,在某层之后的一些层不工作了,那么在训练这些层时,残差函数会趋向0而直接输出 ,也就是短路连接绕过了(或者说屏蔽了)这些(无效的)不工作的层,换言之,残差网络看上去很深,但实际工作的层并没有那么多;
-
网络深度可以无限制的增加,意味着模型可能提取更高层次的特征。
CNN的应用不仅局限于2维度的图像识别领域,也被推广到1维的声音与文字以及3维的影像数据的处理中,比如在医药领域,3维CNN被用来对肺部结节进行排查以及判别肿瘤良性与恶性(在Kaggle和阿里天池机器学习竞赛中)、视频流的分析(时间是第3维度),以及金融指数的预测等。
CNN是深度学习领域最重要的三种模型之一,回顾其发展史可发现:从1980的Neocogition到1999年的LeNet-5经历了20年,再到2012年革命性的AlexNet又经历了10多年,之后发展明显加速,几乎每年都有突破性的新思想被提出来,推动机器学习和AI的迅速繁荣,CNN的发展过程本身也是一个指数发展的过程,目前以分类为目的的CNN已基本完成了历史使命,其他CV方向方兴未艾。
4. 基于Tensorflow-Keras,10行代码搭建CNN
开源深度学习框架 (Deep Learning Framework)能大幅减少深度学习实现过程中重复的工作量,提升开发效率和质量,降低深度学习的门槛。谷歌、Facebook、微软等巨头纷纷推出自己的框架(图3-101),同时,Python已成为最主流的机器学习语言。
Tensorflow是谷歌于2015年11月正式发布的开源通用深度学习框架,由Jeff Dean[20]领导的谷歌大脑团队在谷歌内部的深度学习系统上改进而成,相对于其它框架而言, TensorFlow文档完备,分布式计算效率高,部署方便,虽然推出时间较晚,但却是应用最广的深度学习框架[21]。2017年3月著名深度学习开源库Keras 2.0版成为Tensorflow的一部分,大大简化了深度学习模型的搭建,让没有经验的深度学习用户,也能快速搭建深度学习模型。由于Tensorflow推出的时间较短,研发重心还以实现新功能为主,性能尚有进一步优化的空间。
import keras # 导入Keras时,自动导入Tensorflow
from keras.datasets import mnist # 自带数据集
from keras.models import Sequential # 导入逐层叠加的序列模型
from keras.layers import Dense, Dropout # Dense即全联接模型
from keras.optimizer import SGD # 使用随机梯度下降(SGD)作为优化器
# 定义超参数(Hyper Parameters)
BATCH_SIZE = 128 *#*Mini-batch的批量大小
NUM_CLASSES = 10 *#*0-9 十个数字对应十个分类
NUM_EPOCHS = 20 *#*遍历数据的轮次为20
# 对数据进行随机重排序,生成训练集和测试集
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# 维度转换,将数据从28**28“压扁”(Flatten)为784**1,转换为浮点型
X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)
X_train = X_train.astype(‘float32’)
X_test = X_test.astype(‘float32’)
*# 特征数据规范化,*将在0~255之间的灰度值统一规范至0~1的区间内
X_train /= 255
X_test /= 255
# 将标签数据从0~9转换为 one-hot 变量,比如 2 → [0,0,1,0,0,0,0,0,0,0]
Y_train = keras.utils.to_categorical(y_train, num_classes)
Y_test = keras.utils.to_categorical(y_test, num_classes)
# 搭建ANN模型
model = Sequential() # 顺序叠加的模型是最常用的
# 添加一个全联接层,含512个神经元,激活函数是线性整流函数
# 输入为任何数量的照片,每张照片为784**1
model.add(Dense(512, activation=‘relu’, input_shape=(784,)))
# 再添加一个全联接层,含512个神经元,激活函数是线性整流函数
model.add(Dense(512, activation=‘relu’))
# 输出层Softmax进行多分类
model.add(Dense(10, activation=‘softmax’))
# 编译模型,使用分类交叉熵作为成本函数,Adadelta为优化器
model.compile(loss=‘categorical_crossentropy’,
optimizer=SGD(),
metrics=[‘accuracy’])
# 模型拟合
history = model.fit(X_train, Y_train, batch_size = BATCH_SIZE,
epochs = NB_EPOCHS, verbose = 1,
validation_data=(X_test,Y_test))
经过20次Epoch迭代,在验证数据集上准确率达到了0.9542。
[1]福岛邦彦:人工神经网络先驱之一,日本模糊逻辑系统学院高级科学家,曾任教与东京大学等高校。2003年,获IEEE神经网络先驱奖。
[2]MNIST,拥有60000张训练图像和10000张测试图像,是最大的手写数字图像的数据,常被用来训练和测试图像识别算法。
[3]ImageNet: 目前全球最大的开源的独立于平台的图像数据库,主要被用于机器视觉算法的原型建立。按照词义的层次结构组织,目前拥有12个子树5247个概念和320万张图像,其目标是用1000张图片描述每一个概念,共8万个概念。
[4]深度学习中,常将全连接的神经网络成为“稠密”(Dense)。
[5]为了简化讨论,忽略了偏置(Bias)参数,实际为101个参数。
[6]自上而下4个特征分别为:水平、45度倾斜、垂直和反向倾斜45度。
[7]方括号内两个数字表示过滤器局部感知范围的起点与终点位置。
[8]在CNN处理图像之前,一般会通过预处理将图片处理成常宽像素数量相等的正方形。
[9]考虑到不能整除的情况。
[10]近年来,Dropout被证明是一种更有效的解决过拟合问题的方法,实际利用池化层来防止过拟合已经不多。
[11]该架构对著名的手写数字识别的卷积神经网络LeNet-5的末端全连接部分进行了些许简化。
[12]杨力昆(Yann Lecun)采用的方式是:C3的前6个特征图以S2中3个相邻的特征图子集为输入,接下来6个特征图以S2中4个相邻特征图子集为输入,随后的3个特征图以不相邻的4个特征图子集为输入,最后一个将S2中所有特征图为输入,共16个特征图,详见他与尤舒·本吉奥 (Yoshua Bengio) 等人的论文Gradient-Based Learning Applied to Document Recognition第8页的表1。
[13]如果FC层位于CNN靠近输入的前段,因为降维还不够充分,神经元数量很多,计算量太大。
[14]有一些模型采用双曲正切函数Tanh作为激活函数, 表现通常要优于Sigmoid函数。
[15]ReLU的近似平滑函数是Softplus函数f(x)=ln (1+ ),其导数即为Sigmoid函数。
[16]该网络得名于电影《盗梦空间》英文名称—“Inception”,该影片中有句著名的台词 ¾ “We need to go deeper”(我们需要更深入),这与深度学习需要更深的网络层次的思想非常吻合,V1即第1版。
[17]全连接层几乎占据了AlexNet或VGGNet中90%的参数量,而且可能会导致过拟合,去除全连接层后参数数量大幅度减少,减轻了过拟合,训练速度更快。
[18]Batch Normalization:Inception V2提出的一种很有效的正则化(Normalization)的方法,可提升神经网络模型表现和稳定性,BM对层输入进行标准化,使其均值为0,方差为1。对于一些算法来说,如DCGAN(深度卷积生成对抗网络),BM是必需的。
[19]Juergen Schmidhber(1963-)著名AI科学家,被尊为LSTM之父,瑞士 Dalle Molle学院AI研究机构联合主任,一位常被忽略的深度学习领军人物, 他对深度学习的贡献并不在辛顿与杨立昆教授之下,但因想法太领先时代等原因而没有得到当时学术界应有的重视。
[20]Jeff Dean (1968- ): 美国工程院院士,美国艺术与科学院院士,谷歌大脑负责人,设计和完成了谷歌分布式计算基础,该架构支持了谷歌大部分产品,他本人也被称为“谷歌大脑背后的大脑”。
[21]基于GitHub开源的深度学习项目统计。
[22]杨立昆网站所提供的官方数据集http://yann.lecun.com/exdb/mnist/。
[[i]] Kunihiko Fukushima, Neocognitron: A Self-organizing Neural Network Model for a Mechanism of Pattern Recognition Unaffected by Shift in Position, 1980, http://www.cs.princeton.edu/courses/archive/spr08/cos598B/Readings/Fukushima1980.pdf
[[ii]] Toshiteru Homma, Les E. Atlas, Robert J. Marks II, AN ARTIFICIAL NEURAL NETWORK FOR SPATIOTEMPORAL BIPOLAR PATTERNS: APPLICATION TO PHONEME CLASSIFICATION, 1988, http://papers.nips.cc/paper/20-an-artificial-neural-network-for-spatio-temporal-bipolar-patterns-application-to-phoneme-classification.pdf
[[iii]] Dan Cires¸an, Ueli Meier, Jurgen Schmidhuber, Multi-column Deep Neural Networks for Image Classification, 2012, http://repository.supsi.ch/5145/1/IDSIA-04-12.pdf
[[iv]] Yann LeCun, Leon Bottou, Yoshua Bengo et al. Gradient-Based Learning Applied to Document Recognition, 1998, http://yann.lecun.com/exdb/publis/pdf/lecun-01a.pdf